Meeting in the middle
Charlie and Gabriel are walking towards each other's houses. What is the chance that they'll meet along the way?
Problem
Charlie and Gabriel live in opposite corners of a town. The town is built on a grid system, and the roads look like this:
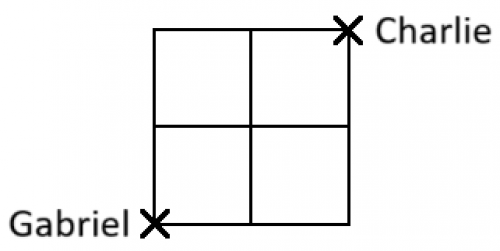
Charlie and Gabriel leave their houses at the same time. Each begins to walk towards the other's house by walking along the sections of road, moving at the same speed. They always take the shortest route possible (and at every crossroads they make their next choice randomly, if there are multiple shortest routes).
What is the probability that they will meet at some point in the journey?
How does the probability change if the size of the grid increases to three squares by three squares? What about four squares by four squares?
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible support
Possible extension
Submit a solution
What we like to see
We have written an article on what we are looking for when we decide which solutions to publish.
You can share your work with us by typing into the form above or uploading a file.
What can I upload?
- Word documents
- PDF files
- Excel spreadsheets
- Images, including screenshots or photos of written work
If your work is on another app
You can also send us a link to your work on:
- Youtube/Vimeo
- Google Docs
- Sharepoint/Office 365
- Anywhere sensible on the internet!
Please make sure you have set the permissions so that we can access your work.
How we use your information
By uploading your solution here you are giving us permission to publish your work, either as a whole or edited extracts, on the NRICH website and in associated educational materials for students and teachers, at our discretion.
For our full terms of use regarding submitted solutions and user contributions please see https://nrich.maths.org/terms.
Your information (first name, school name etc) is optional. If supplied, it may be used for attribution purposes only if your work is published on the website. Data that you supply on this form (e.g. age if supplied, location if supplied) may also be anonymised and used for evaluation and reporting.
For more information about the University's policies and procedures on handling personal information, and your rights under data protection legislation, please see https://www.information-compliance.admin.cam.ac.uk/data-protection/general-data.
