The Farmers' Field Boundary
The Farmers' Field Boundary printable sheet
Two farmers each have a field with a shared boundary. On the boundary is a tap.
The farmers decide it would be more convenient if the boundary was a straight line, but they both need to access the tap.
Your challenge is to redraw the boundary so that:
- Both farmers can access the tap
- The boundary line is straight
- The new fields have the same areas as the original fields
You can use the interactivity below to explore this problem with a variety of fields.
Move the points to create two fields, then click Fix Fields.
Once you have created your fields, a purple dot will appear which you can move to create the new field boundary.
When you think your new fields have the same area as the original fields, you can tick the "Show areas" box to see how close you are.
Can you come up with a geometrical method for constructing the position of the new boundary?
Can you adapt your method to construct a boundary for a more complicated situation like the one pictured below?
Can you describe a method for redrawing boundaries with four, five, or more straight lines into a single straight line?
Can you find other triangles (with the red line as their base) that have the same area as the triangular part of the field on the right?
Are there any parallel lines we can draw that might help?
What do we know about triangles with the same base and the same perpendicular height?
This was a fascinating problem which included an interactive feature to help you explore your ideas.
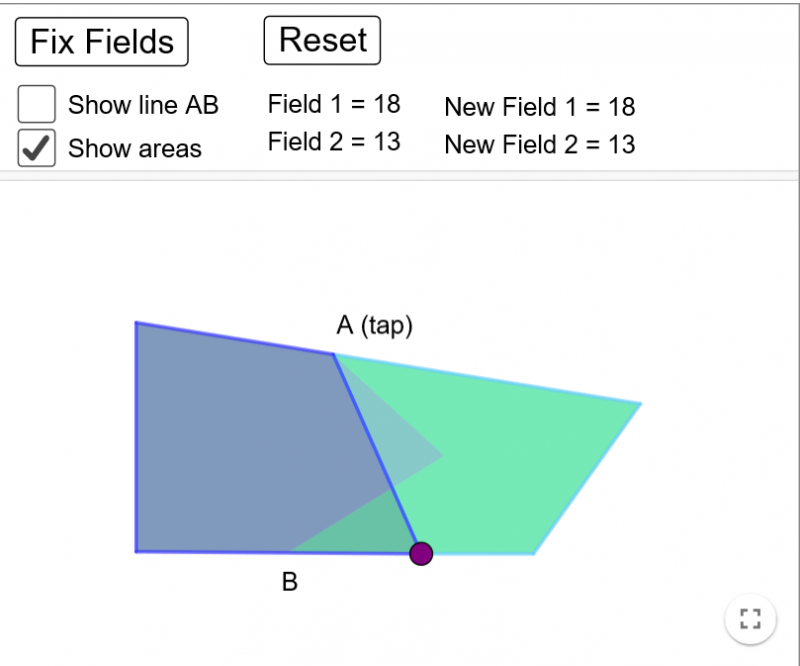
Let's begin by looking at the first part of the problem. You needed to use the interactivity to create two fields which shared the tap at A and maintained the same areas.
Here's a screenshot of a solution sent in by from Shriram, from India:
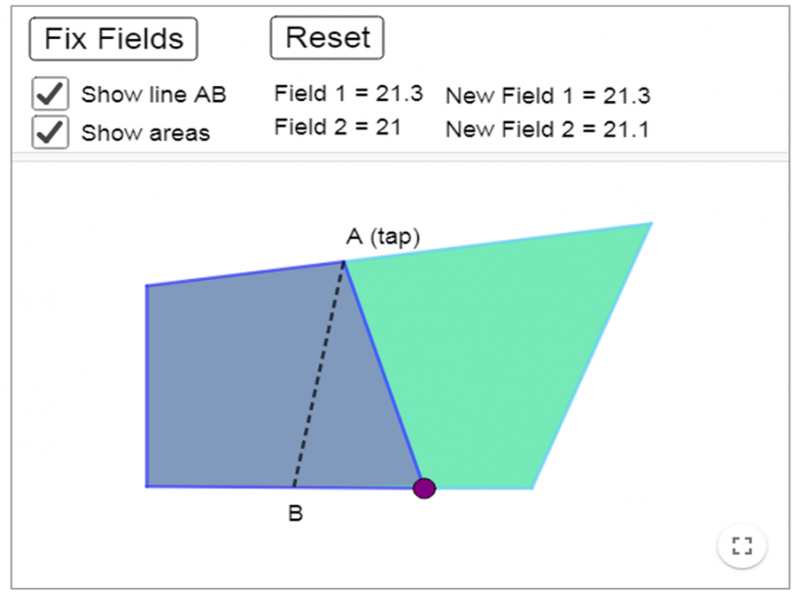
Zavya, Miraya and Methuli from Heckmondwike Grammar School in Engliand also sent in screenshots. This is one of Zavya's screenshots:
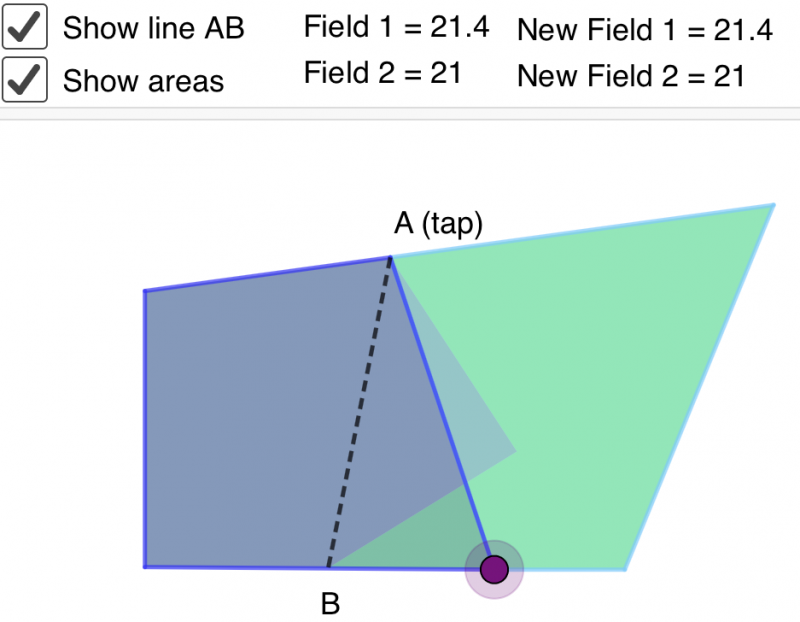
This is one of Methuli's screenshots:
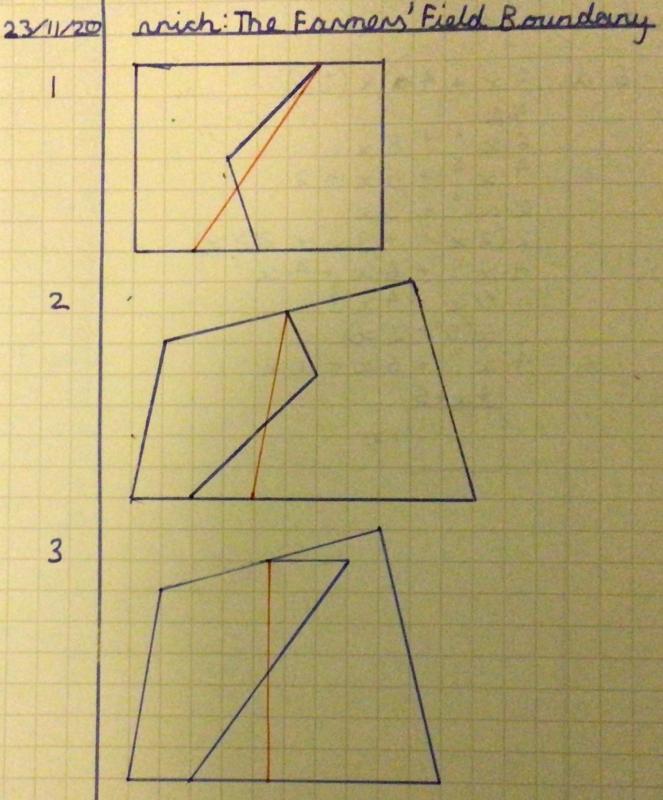
Miranda sent in some correct solutions drawn by hand but didn't explain her method:
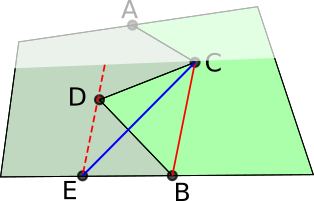
Kirsty from Lancing College and David from the UK explained how to form the correct boundary. Here is David's work:
If they do have the same area, then line AB' is the new boudary. This is because changing from ACB to AB, the farmer on the left loses triangle ABC. Then changing the boundary from AB to AB', the farmer on the left gains ABB'.
Clearly, they both share the same base AB. Furthermore, as AB is parallel to CB' (by construction), the area of triangle ABB' is the same as the area of triangle ABC. This is because a triangle's area can be determined solely from $0.5\times\text{base}\times\text{perpendicular height},$ and the two perpendicular heights in this case are the perpendicular distances between two parallel lines (which are constant). So AB' is the required straight line.
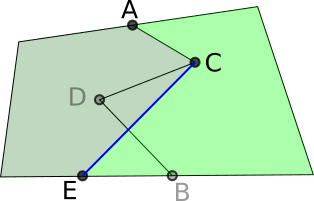
Kirsty extended this idea to fields with more complicated boundaries. Here is Kirsty's work with a couple of extra diagrams added:
Why do this problem?
This problem presents a geometrical situation which can be solved using constructions. The interactive environment gives students the opportunity to explore and make conjectures which they can go on to justify, using what they know about areas of triangles.
Possible approach
Explain the context of two farmers who wish to redraw their boundary, keeping the field areas the same, but making the boundary a single straight line. Add the extra constraint that one end of the line must be by the tap. Then give students some time to explore the interactive environment in pairs. They can set up various configurations of the two fields and then try to position the boundary correctly. Once they think they have positioned the boundary in the right place, there is the option to reveal the actual areas to see how close they are to the desired boundary.
When everyone has had a chance to explore, encourage them to start thinking about how to find the solution using geometrical reasoning rather than just guesswork. One possible approach is to encourage them to collect screenshots of correct solutions so they can look at several examples at once. The interactivity offers the option to draw the line AB, which might prompt some students to imagine lines parallel to AB that provide useful information when looking for a way to conserve the original areas.
The problem Shear Magic might offer students useful insights about families of triangles with the same base and a third point moving along a line parallel to the base. These insights can then be used to justify their method for constructing the new boundary.
Once students have come up with a method for solving this type of problem, they could have a go at constructing solutions away from the computer.
Here is a worksheet with three examples of fields that students could construct the new boundary on: Farmers' Fields
There is also a version without grids: Farmers' Fields (without grid)
Here is sheet showing the answers to the three examples: Farmers' Fields Answers
Key questions
Approximately where does the line need to go?
Are there any parallel lines we can draw that might help?
What do we know about the area of triangles with the same base and height?
Can we transform the triangle with base AB into an equivalent triangle with the same area?
Possible support
It might be worth working on Shear Magic before trying this problem.
Encourage students to start with rectangular field boundaries like the first example on the Farmers' Fields worksheet.
Possible extension
Triangle in a Triangle and the problems that follow it require similar geometrical reasoning but provide a more challenging exploration.