Magical Products
Can you place the nine cards onto a 3×3 grid such that every row, column and diagonal has a product of 1?
Problem
Put the nine numbers below onto a 3 by 3 grid so that each number occupies one space, and the product of every row, column and diagonal is equal to 1.
$$1 2 3 6 \frac{1}{6} \frac{1}{3} \frac{1}{2} \frac{2}{3} \frac{3}{2}$$
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
This is one answer (seven others are possible by rotation and reflection)
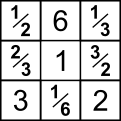
Put the 1 in the middle so that reciprocals can go opposite each other.
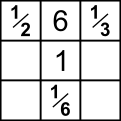
Try placing the 6 at a corner:

$\frac 16$ must go opposite $6$

$\frac12$ and $\frac13$ must go next to $6$ to multiply to $1$
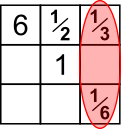
But $\frac13$ is opposite $\frac16$ and there is nothing large enough to multiply by to get $1$
$\frac12\times\frac16$ is also too small so swapping $\frac12$ and $\frac13$ would not help
Try placing the $6$ in the middle of an edge: