Four or Five
The diagram shows a large rectangle composed of 9 smaller rectangles. If each of these rectangles has integer sides, what could the area of the large rectangle be?
Problem
The diagram shows a large rectangle composed of nine identical smaller rectangles.
Image
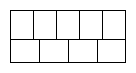
Both the length and breadth of each of these smaller rectangles are whole numbers of centimetres. Which of the following could be the area of the large rectangle?
a. 450 square centimetres
b. 1260 square centimetres
c. 1620 square centimetres
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
Answer: 1620 square centimetres
Using the options given
450 $\div$ 9 = 50
50 = length $\times$ width, where length : width = 5 : 4
50 = 5 $\times$ 10
No closer factor pairs $\therefore$ no factor pairs in the ratio 5 : 4
1260 $\div$ 9 = 140
140 = 2 $\times$ 70
= 4 $\times$ 35
= 10 $\times$ 15
No closer factor pairs $\therefore$ no factor pairs in the ratio 5 : 4
1620 $\div$ 9 = 180
180 = 10 $\times$ 18
= 12 $\times$ 15 correct ratio
So 1620 is possible
Using $x$
The ratio length:breadth of the smaller rectangles is $5:4$. Let the length and breadth of these rectangles be $5x \; \text{cm}$ and $4x\; \text{cm}$ respectively. The area of the large rectangle, in cm$^2$, is $9 \times 20x^2 = 180x^2$ and the only one of the alternatives which is a product of $180$ and a perfect square is $1620$, which corresponds to $x = 3$.
