Hexy-metry
A hexagon, with sides alternately a and b units in length, is inscribed in a circle. How big is the radius of the circle?
Problem
Hexy-metry printable sheets: main problem, idea cards
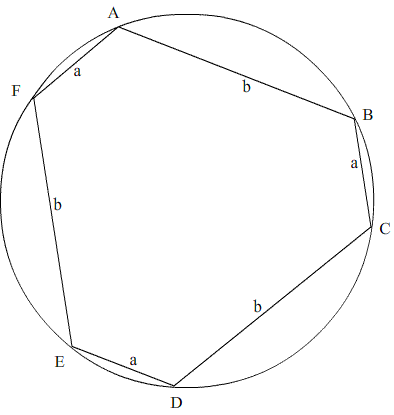
Explain how you worked out your answer.
Getting Started
Make cards from the images in this document .
Do they help you to make connections?
Can you arrange them in ways that help you to see some of the properties of the problem image?
Student Solutions
This very good solution came from The Maths Club at Wilson's School :
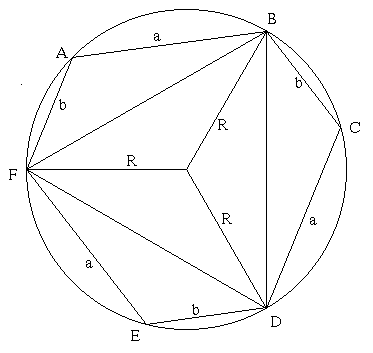
The interior angles of the hexagon are all equal to 120 degrees by symmetry.
Let O be the centre of the circle, with radius $r$. Considering triangle BCD, by the cosine rule,
$$BD^2 = a^2 + b^2 - 2ab \cos 120.$$
Considering triangle BOD, by the cosine rule,
$$BD^2 = 2r^2 - 2r^2 \cos 120.$$
As $ \cos 120 = -\frac {1}{2}$, we have $a^2 + b^2 + ab = 3r^2$ so
$$r = \sqrt {{a^2 + b^2 + ab\over 3}}.$$
Ruth from the Manchester High School for Girls proves the figure has rotational symmetry of order 3 and the angles are 120 degrees as follows, and then goes on to find the solution using the Cosine Rule as above:

Teachers' Resources
Why do this problem?
This problem requires the solver to reason geometrically and make use of symmetry. By re-presenting the information in a different way, for example by adding additional lines (a useful technique in geometrical problems) more structure can be revealed. It is an interesting idea that adding something, and therefore apparently making it more complex, can sometimes make a problem more accessible. Then of course there is an opportunity to use the cosine rule in a non-standard context.
Possible approach
Using the idea cards, display the problem and ask learners to work in groups rearranging the cards in ways which help to make connections for them. Members of the group should explain their ideas to their group, and the group should agree on cards that go together, or complement each other.
Share ideas and relationships that groups notice before going on to solve the problem. Encourage careful reasoning and convincing arguments. For example:
- "Why can you say those two angles are equal?
There are several ways of solving the problem so share different approaches and discuss what helped to move thinking forward.
Two observations may be worth drawing attention to :
- the reflection symmetry between $a$ followed by $b$ and $b$ followed by $a$,
- the angle at the circumference as half the angle subtended at the centre onto the same arc (in this case an arc greater than a semicircle) .
Key questions
- How can you use the symmetry of the figure to determine some of the angles ?
- What things in the images helped to make connections for you?
- What do we need to find, and can that be found directly ?
Possible support
Ask the students if they can explain why these should all be equal .
Possible extension
