Napier's Bones
Problem
The Scot, John Napier, invented these strips (originally made from bone) about 400 years ago to help calculate multiplication and division.
This is what they looked like:
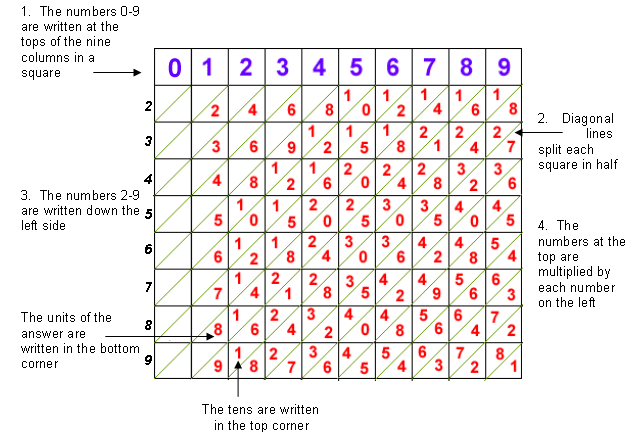
Can you work out how to use Napier's bones to find the answer to
24 x 6?
How about 461 x 4?
Now try 8931 x 6.
Can you work out how you would use them to calculate the product of 3541 and 768?
Getting Started
The table is split up into the nine columns. Here is how they're used:
For example, let's calculate 32 x 7 .
Lay out the two strips showing 3 and 2 at the top like this:
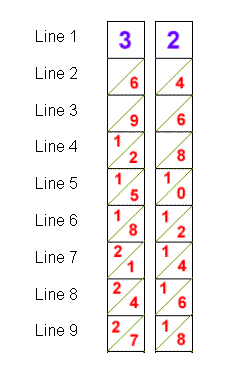
To multiply this number by 7, add the numbers along the diagonals of the seventh line, starting at the right:
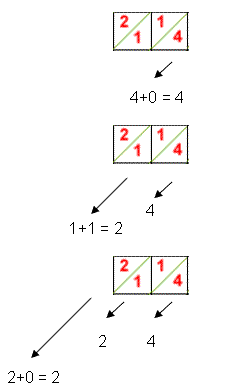
So the answer is 224 .
Student Solutions
Clement from Shat Tin College in Hong Kong has sent us a detailed explanation of how to use Napier's Bones to calculate the products in the question:
In order to work out a multiplication such as 8931*6, you need
to first work out 8*6.
Taking the first digit of the 4 digit number and multiplying it by
6 which gives you 48.
You then do the next digit, 9*6 which gives you 54.
You add the first digit of 54: 5 to the last digit of 48: 8. This
gives you 13.
You then add the tens digit of 13: 1 to the very first digit: 4
which than gives you a total of 534.
You carry on with 3*6: 18, add the tens digit: 1 to the last digit
of the total: 534 giving you 535 and put the unit: 8 at the end.
5358.
The last step is 1*6, adding the answer: 6 to the total: 5358 gives
you 53586.
The answer for 461*4 was 1844 and the answer for 24*6 was 144.
The last one was very complicated, 3541*768:
Firstly, you multiply the four digit number, 3541 by the first
digit of the 3 digit number, 7. But remember to use Napier's bones
to do this multiplication step by step in the way I explained in
the first paragraph. You get 24787.
Then multiply 3541 by the next digit of the 3 digit number, 6. This
gives you 21246.
The next step is to multiply 3541 by the last digit of the 3 digit
number, 8. That makes 28328.
You add this to the previous answer: 21246 starting from the second
digit, for example: 21246 + 28328 but keep the 2 at the front of
21246. This makes 240788.
The last step is to add this number to 24787, the first answer,
starting from the second digit for example: 24787 + 240788 but
keeping the 2 at the front of 24787.
This makes 2719488.
Excellent Clement, you have written a clear explanation which must have been hard without any pictures.
