The root of the problem

Pablo from King's College Alicante, Shehan from Brooke Weston Academy, NF from Eton, Edward from Merchiston Castle School, Sebastian, Josh from the Dukeries Academy, Charlie and Fasai from Ms Brown's class at Bangkok Patana School, Anny from St Mary's School Cambridge, Rajesh from MJV College of Engineering, Siddhant from Indus International School of Bangalore, Sonakshi from Manly Selective Campus, Deborah from Woodford County High School, Kian from Sir Henry Floyd Grammar School, Ammu and Jennifer from St Monica's RU High School, Haochen from TSS and Nharen, Danny and Mete from Dulwich College (Singapore) began by rationalising the denominators of the terms in the sum. This is some of Deborah's work:

Image

                         

Image

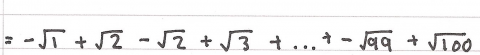
Josh kept the terms grouped in their fractions and wrote this sum as

$(\sqrt2-\sqrt1)+(\sqrt3-\sqrt2)+(\sqrt4-\sqrt3)+...+(\sqrt{a}-\sqrt{a-1})+...+(\sqrt{100}-\sqrt{99})$

From here, the sequence can be quickly simplified. In the first term, $\sqrt2$ appears and in the second term, $-\sqrt2$ appears. This means that the $\sqrt2$ can be eliminated from the sequence. This elimination is possible for all of the square roots except for the $-\sqrt1$ in the first term and the $\sqrt{100}$ in the last term due to there being a $\sqrt a$ and a corresponding $-\sqrt a$ for all square roots except these two.

This leaves us with a simplified sequence of $-\sqrt1+\sqrt{100}$, which can be simplified to $-1+10$, which is equal to $9$. Therefore, the solution to this sequence is $9$.

Kai from BISS Puxi began by adding the terms from the beginning:

If we [rationalise the denominator and simplify] the firt term, we get $\sqrt2-\sqrt1$.

If we continue this on the second term it will turn into $\sqrt3-\sqrt2$.

When they are added, we get $\sqrt3-1$.

As the pattern repeats, towards the end we will be left with $\sqrt{100}-1$,

which is equal to $9$.

 

Mitali from Delhi Public School Sushant Lok, Niccolo from West Bridgford School and Polina and Luis from King's College Alicante considered a more general case. This is Niccolo's work:

Since the numerator of each of these fractions is $1$, rationalizing each fraction will result in a series of fractions in the form: $$\frac{1}{\sqrt a+\sqrt b}=\frac{1(\sqrt a - \sqrt b)}{(\sqrt a+\sqrt b)(\sqrt a - \sqrt b)}=\frac{\sqrt a -\sqrt b}{a-b}$$

Given that, for each fraction, $a$ and $b$ are consecutive, $a-b$ will always be equal to $-1$, hence the denominator is always $-1$. Division by $-1$, of course, simply inverses positives and negatives on the numerator, as such: $$\frac{\sqrt a - \sqrt b}{-1}=-\sqrt a+\sqrt b$$

If all the fractions are rationalised in this way, the expression will be: $$-\sqrt1+\sqrt2-\sqrt2+\sqrt3-\sqrt3+\sqrt4...+\sqrt{100}$$ Now there are pairs of surds which cancel each other out, leaving only: $$-\sqrt1+\sqrt{100}=-1+10=99$$

William from Bishop Wordsworth's School used this algebra mixed with Kai's method of adding the terms from the beginning:

Image

 

Adam from Methodist College Belfast, Tariq from City of Leicester College, David from Bangkok Patana School, Eliza from Latymer Upper School, Kevin and Xavier from Kimberley College, Luke from Cedars Upper School, Rhys from Comberton Village College and Daniel from Eastbury Community School considered a general term in the sum. This is Eliza's working:

$$\frac{1}{\sqrt n +\sqrt{n+1}}\\=\frac{1}{\sqrt n +\sqrt{n+1}}\frac{\times(\sqrt n-\sqrt{n+1}}{\times(\sqrt n-\sqrt{n+1}}=\frac{\sqrt n-\sqrt{n+1}}{n-(n+1)}=\frac{\sqrt n-\sqrt{n+1}}{-1}=\sqrt{n+1}-\sqrt n$$ So the sum becomes

$$(\sqrt{n+1}-\sqrt {n})+(\sqrt{n+2}-\sqrt{n+1})+(\sqrt{n+3}-\sqrt{n+2})...(\sqrt{n+99}-\sqrt{n+98})$$ where $n=1$, $$=-\sqrt 1 +\sqrt{100}=10-1=9$$

Max from Westminster, Amrit from Hymers College, Peter from Heaton Manor and Sebastian all used summation notation. This is Amrit's work:

$$\begin{split}\frac1{\sqrt1+\sqrt2}+\frac1{\sqrt2+\sqrt3}+...+\frac1{\sqrt{99}+\sqrt{100}}&=\sum_{i=1}^{99}\frac1{\sqrt{i}+\sqrt{i+1}}\\

&=\sum_{i=1}^{99}\frac{\sqrt{i}-\sqrt{i+1}}{(\sqrt{i}+\sqrt{i+1})(\sqrt{i}-\sqrt{i+1})}\\

&=\sum_{i=1}^{99}\frac{\sqrt{i}-\sqrt{i+1}}{-1}\\

&=\sum_{i=1}^{99}\sqrt{i+1}-\sum_{i=1}^{99}\sqrt i\\ \end{split}$$

Here, Amrit changes the limits, so that instead of going from $1$ to $99$, $i$ goes from $0$ to $98$. In the first sum, this means that the term for $i=0$ must be subtracted and the term for $i=99$ must be added to avoid changing the value of the sum. For the second sum, the expression changes, since to get the numbers $1,...99$ from $i=0,...98$, we would need to use $i+1$ instead of just $i$.

$$\begin{split}&=\left(\sum_{i=0}^{98}\sqrt{i+1}-\sqrt{0+1}+\sqrt{99+1}\right)-\sum_{i=0}^{98}\sqrt{i+1}\\

&=\sum_{i=0}^{98}\sqrt{i+1}-\sum_{i=0}^{98}\sqrt{i+1}-\sqrt{1}+\sqrt{100}\\

&=\sqrt{100}-\sqrt1\\

&=9

\end{split}$$

Nharen, Danny and Mete showed what happened if they changed the sum:

Any fraction similar to this will equal an integer if the first surd and the last surd are square numbers.

For example: $$\frac1{\sqrt4+\sqrt5}+\frac1{\sqrt5+\sqrt6}+...+\frac1{\sqrt{143}+\sqrt{144}}$$ After rationalising, this becomes: $$\frac{\sqrt4-\sqrt5}{-1}+\frac{\sqrt5-\sqrt6}{-1}+\frac{\sqrt6-\sqrt7}{-1}+...+\frac{\sqrt{143}-\sqrt{144}}{-1}$$ This gives you $\dfrac{\sqrt4-\sqrt{144}}{-1}$ and if you simplify that you get $\dfrac{2-12}{-1}=10.$

Pablo, David and Xavier extended the sum to $n$. Xavier said:

This means that for the series in this form for the first $n$ natural numbers the sum is the root of the last value ($n$) minus $1$:

$$\frac{1}{\sqrt1+\sqrt2}+\frac{1}{\sqrt2+\sqrt3}+...+\frac{1}{\sqrt{n}+\sqrt{n+1}}=\sqrt{n}-1$$

Josh tried changing the numbers in the terms:

This rule would work for any sequence with terms such as $$\frac1{\sqrt a +\sqrt b}+\frac1{\sqrt b+\sqrt c}+...+\frac1{\sqrt y+\sqrt z}$$ For the solution to have a whole number, $-\sqrt a+\sqrt z$ would have to equal a whole number. For example, the sequence $$\frac1{\sqrt4+\sqrt7}+\frac1{\sqrt7+\sqrt{10}}+...+\frac1{\sqrt{166}+\sqrt{169}}$$ would have a whole number solution of $11$ because the sequence could eventually be simplified to $-\sqrt4+\sqrt{169}$, which equals ${11}$.

Pablo also considered deciding what the value of the sum of the original series continued to $\sqrt n$ should be, and looked at what happens if we change the 'gaps':

$$\begin{align}&S = (\sqrt2 - \sqrt1) + (\sqrt3 - \sqrt2) + ... + (\sqrt{n} - \sqrt{n-1}) + (\sqrt{n+1} -

\sqrt n)\\

\Rightarrow&S = -\sqrt1 + (\sqrt2 - \sqrt2) + (\sqrt3 - \sqrt3) + ... + (\sqrt n - \sqrt n) + \sqrt{n+1}\\

\Rightarrow&S = \sqrt{n+} - \sqrt1\\

\Rightarrow&S = \sqrt{n+1} - 1\end{align}$$

(where $S$ is the sum)

Therefore, to create a series that adds up to a value $S$, the number of terms can be found by rearranging the equation:

$$\begin{align}S+1& = \sqrt{n+1}\\

\Rightarrow(S+1)^2 &= n + 1\\

\Rightarrow n& = (S+1)^2 - 1\end{align}$$

If we pick a positive integer value for $S$, $S + 1$ will also be an integer, and so will its square. Additionally, adding one to that will still give a positive integer. This means that given enough terms the series can add up to any positive whole number.

It can be generalised further, by considering gaps larger than one between surds in the denominators.

For example:

$\dfrac1{\sqrt1 + \sqrt3} + \dfrac1{\sqrt3 + \sqrt5}$ has gaps of two

This changes things because now the denominator will be two:

$(\sqrt3 + \sqrt1)(\sqrt3 - \sqrt1) = \sqrt3\sqrt3 - \sqrt1\sqrt3 + \sqrt1\sqrt3 -\sqrt1\sqrt1 =

(\sqrt3)^2 - (\sqrt1)^2 = 3 - 1 = 2$

For the numerators, we wil get:

$(\sqrt3 - \sqrt1) + (\sqrt5 - \sqrt3) = \sqrt5 - \sqrt1$

So in total the sum will be

$\dfrac{\sqrt5 - 1}2$

Now this wasn't a rational number, because the last number ($5$) wasn't a square number, if we had reached up to $\dfrac1{\sqrt7 + \sqrt9}$, the sum would've been $\dfrac{\sqrt9 - 1}2 = 1$

So, for a series like the one in the questions with gaps of $a$, the $n^{\text{th}}$ term will be:

$$\dfrac1{\sqrt{1+na} + \sqrt{1+(n+1)a}}$$

If we add up the series up to the $n^\text{th}$ term, the numerators will look like this:

$$\left(\sqrt{1+a} - \sqrt1\right) + \left(\sqrt{1+2a}- \sqrt{1+a}\right) + ... + \left(\sqrt{1+(n+1)a} -

\sqrt{1+na}\right)$$

All the surds will cancel out except for $\sqrt1$ and $\sqrt{1+(n+1)a}$, leaving:

$$\sqrt{1+(n+1)a} - 1$$

When the gap between surds was $1$, once rationalised the denominator became

$1$. When the gap was $2$, the denominator was also two. So if the gap is $a$,

the denominator will become $a$:

$y = x + a$ where $a$ is a positive integer

$$\begin{split}\left(\sqrt y + \sqrt x\right)\left(\sqrt y - \sqrt x\right) &= \left(\sqrt y\right)^2 - \left(\sqrt x\right)^2\\& = \left(\sqrt{x+a}\right)^2 - \left(\sqrt x\right)^2\\

&= \left(x + a\right) - x \\&= a\end{split}$$

Then, if we divide by $a$ (the denominator), the sum will be:

$$S = \dfrac{\sqrt{1+(n+1)a} - 1}a$$

Let's check with a sum we know the value of, the one in the question. $a = 1$

$$\begin{align}\sqrt{1+(n+1)} &= \sqrt{100}\\

\Rightarrow1 + n +1 &= 100\\

\Rightarrow n &= 98\end{align}$$

$$\begin{align}

&S = \dfrac{\sqrt{1+(98+1)\times1} - 1}1\\

\Rightarrow&S = \frac{10 - 1}1\\

\Rightarrow &S = 9\end{align}$$

This is the same as the answer we got manually.

If we solve for $n$:

$$\begin{align}&S = \frac{\sqrt{1+(n+1)a}- 1}a\\ 

\Rightarrow &aS = \sqrt{1+(n+1)a} - 1\\

\Rightarrow&aS + 1 = \sqrt{1+(n+1)a}\\

\Rightarrow&(aS + 1)^2 = 1 + (n+1)a\\

\Rightarrow&(aS + 1)^2 - 1 = (n+1)a\\

\Rightarrow &a^2S^2 + 2aS + 1 - 1 = (n+1)a\\

\Rightarrow &a^2S^2 + 2aS = (n+1)a\\

\Rightarrow&aS^2 + 2S = n + 1\\

\Rightarrow&n = aS^2 + 2S - 1\end{align}$$

Say we want the series to add up to $7$:

$$\begin{align}&n = a(7)^2 + 2(7) - 1\\

\Rightarrow& n = 49a + 13\\

\Rightarrow &n - 49a = 13\end{align}$$

This can be plotted as a graph (in the $x$-$y$ plane) and you can manually look for integer solutions. The easiest solution is when $a = 1$, ie our initial sequence (the one proposed in the question). Because the coefficient of $n$ is $1$, all integer values of $a$ are solutions.