Lawnmower
Problem
A kite shaped lawn consists of an equilateral triangle ABC of side 130 feet and an isosceles triangle BCD in which BD and CD are of length 169 feet. A gardener has a motor mower which cuts strips of grass exactly one foot wide and wishes to cut the entire lawn in parallel strips. What is the minimum number of strips the gardener must mow?
Student Solutions
Tony Cardell, has sent in this solution, which gives the correct answer. We're still not quite convinced: how does he know that the strips are parallel to the longer side? If anyone can explain this, we'll add their explanation here.
We must find the maximum distance between a pair of opposite sides (it doesn't matter which since this is a kite). If we extend the two sides (coloured blue), the intersection is on the same side of the kite as the equilateral triangle, as shown. So the maximum distance between the two sides is the red line.
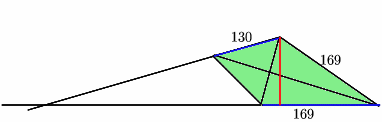
Now look at the isosceles triangle part of the kite. One formula for the area of a triangle with sides a,b,c says that if s is the semi-perimeter, (a+b+c)/2, then the area is the square root of s(s-a)(s-b)(s-c). The isosceles triangle has sides 169, 169, 130, so s=234 and the area is 10140 square feet. But we also know that the area is 1/2 x base x height, so the height we want is 10140 x 2 / 169=120. So 120 foot-wide strips will be needed.
