Great squares
Problem
I was doodling the other day and drew a little square like this:-
I supposed that the side was one (something) long. Well I wondered what would happen if I drew the four lines a bit longer, in fact twice as long so that the extra bits stuck out.

This was quite a nice little design, I thought, and then I noticed that it looked at though the ends of these lines looked as though they could make a square. So I drew one! I've used a different colour to show this new square.

Now, mathematical patterns usually go on repeating themselves so I used that idea to pretend that this new green square was my first one and so I drew the extra bits again, so that the lines were twice as long as the square.

So I went on!
A new square appeared, now red!

Extend that one. . .

I really liked what was happening here!
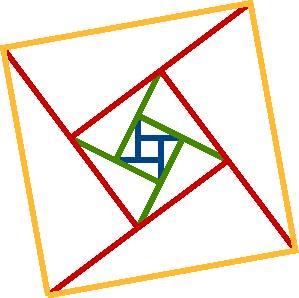
and so on. . . .


I had to stop there because it had up to the size of the paper.
I suggest that you print these pages out so far and have a good look at the way that the pattern has grown and see what things you notice in this last picture.
When I looked at this shape I could imagine that I was looking through a square window at a pattern of squares but could only see the one square in the middle.
So I printed out these:-

Then I printed out the bigger square . . . .

This one I traced onto a "see through" sheet and placed it in different places over the grid of smaller squares.
This was great fun and led to some interesting conversations. Have a GO!
I think that this is one of the most exciting shape investigations that I've put on the NRICH site, so let's have a lot of workings sent to Cambridge U.K. from all over the world so that we can show how people from different countries are thinking and working in their maths. Pester your teachers to collect some results and send them off.
Student Solutions
There are lots of answers to this problem, depending on what questions you choose to ask.
Have a go yourself, and if you discover anything interesting, e-mail us to tell us what you've done! Please don't worry that your solution is not "complete" - we'd like to hear about anything you have tried. Teachers - you might like to send in a summary of your children's work.
