Prompt Cards
These two group activities use mathematical reasoning - one is numerical, one geometric.
Problem
Can you work out what Charlie's number is from these clues?
- C1: Charlie's number is palindromic, the second and third numbers are different.
- C2: Charlie's number is greater than 100 and is prime.
- C3: Charlie's number is odd. The difference between the largest and smallest digits is 5.
- C4: Charlie's number is less than 1000. The sum of the digits is 14.
- C5: Charlie's number is not divisible by 3. It is less than 500.
- C6: Charlie's number is a whole number with only two divisors.
Now can you make this tower from coloured cubes? Or, if you don't have any cubes, you could draw it.
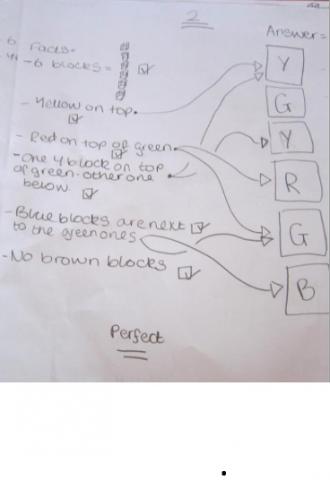
- C1: There are six blocks in the tower, a yellow one is at the top.
- C2: The red block is above the green block.
- C3: One of the yellow blocks is above the green block, the other is below it.
- C4: Each of the blue blocks shares a face with the green block.
- C5: No two blocks of the same colour touch each other.
- C6: There are no brown blocks in the tower.
Student Solutions
Ruby W and Ruby F from Hadnall CE Primary School tried both challenges;
Charlie's Number
"Using clues 2 and 4, we realised that our number had to be 3 digits long. Using clue 3, we initially worked out that our number need to end in 3, 5, 7 or 9. As Charlie's number is palindromic, the third and first digits need to be the same. Therefore, due to rule 5, our first and third digits had to be 3 (to make sure our number is less than 500). Finally, using rule 3, we used 8 as our second digit (to make the difference between the largest and smallest digits 5). We used the rest of the rules to check our number to see if it worked. 383 is a prime number and therefore will only have two divisors (itself and one and NOT 3)."
Tower problem
"Rule one meant we started with a yellow cube on top. We then placed a red cube on top of a green cube and placed this below the yellow - for rule two and part of rule three. We both blue cubes on the outside faces of our green cube - for rule four. Finally, we placed a yellow cube underneath the red to satisfy all the rules. Realising that "above" did not necessarily mean "directly above"/"touching", made this problem a lot easier.
We then tried to create a tower which was a single cube wide. By placing both blue cubes either side of the green cube, we satisfied rule 4. Placing a red cube above a blue cube satisfied rule two. Placing a yellow cube on the top and bottom of the tower satisfied the remaining rules."
James Huggins from Norman Gate School wrote;
Using the information I had, I created different numbers which were over 100 and prime. Then I checked to see whether the difference between the largest digit and smallest digit was 5. I then checked to see which of these numbers had a total of 14, very quickly I could see the answer was likely to be 383. This number has no decimal places and was odd. I tried to divide this number by 3, 7 and 9 to double check it was prime. I knew it wouldn't be divisible by 5 because it didn't end with a 5 or 0. I knew it wasn't divisable by 4, 8, 6 or 2 as it was an odd number. 383 is over 100 and under 500.
Frances and Charlie from Millfields Primary School sent in the following;
We followed the clues one by one and wrote down a number which satisfied that criteria. When we looked at the next clue, we adjusted and changed our numbers; we kept doing this until we reached the last clue. We were amazed that we had found an answer which worked for all the clues. We could not find another number which worked - everyone in our class had a go and
no-one succeeded!
Farha from Arnhem Wharf Primary School wrote;
My starting point was clue 4. Since I knew the sum has to be 14 and from clue 3 the difference had to be 5. I started using random numbers. For example: 626 but the difference here is 4. Then I used 8 and 8-5=3. So far my numbers were 3 and 8. 3+8=11 and I need 14 so I just added 3. At the end my numbers were 383. I've checked 383 with all the clues and it matches them all.
Zahara also from Arnhem Wharf Primary School wrote;
I started off by listing the prime numbers from 1 to 9: 2, 3, 5 and 7. After I listed the numbers I crossed out the even prime number(s): 2. Clue number one it tells me it should be a palindromic number, so the number at the end should be the first digit as well (and possibly the second). Thanks to clue number five I knew that the number should not be over 500 therefore eliminating 7 and 5. I then knew the number had to be 3_3 or 333 but then realised the difference between the largest and smallest number must be five, from clue 3, and decided it could not be 333. So I did 3+5 which equals 8. I came to the conclusion that the answer was 383 but I wanted to check whether it would add up to 14 (3+3+8), which clue 4 mentions. The
numbers did add up to 14 meaning the answer is 383.C
Mrs Morris and Mrs Cave's Year 4 Maths class at Darras Hall First School said;
After reading the clues we split into 4 groups to look at numbers from 100-200, 200-300, 300-400 and 400-500 as we knew that Charlies number was between 100 and 500. We looked for prime numbers first. We quickly realised that Charlie's number couldn't be in the 200s or 400s because it would then end in a 2 or a 4 because it was palindromic and it would then be an even number. We then realised that Charlie's number couldn't be in the 100s because it would then have a 1 in the hundreds and units and in order to add up to 14 the middle digit would have to be 12, which is impossible. We then knew the number had to start and end in a 3, which would mean that the middle digit would have to be an 8 in order to add up to 14. We also knew that the difference between 3 and 8 is 5. After testing all the other criteria we know that Charlie's number is 383!
Claudia and Trudie from Maltmans Green worked in a different way.
1.First write down all the palindromic numbers between 100-500
2.Then cross out all of the even numbers on your list
3.With the numbers left, add all the digits (of each number) together and see if they add up to 14. If they don't them cross them off
4.After, divide the number (which is left) by 3 and see if the answer is a whole number
5. If the answer is not a whole number then that is the answer to the problem
For the 2nd part we also had Daanya and Elodie from Maltmans, here is their work;


Tianyi from Morley Memorial Primary School wrote;
It is 383.
1) hundred: x; tenth:y. digit: z 2) x+y+z=14, 3) 100 4) Primes 167,239,257,293,383,419,491
5) biggest-smallest = 5 257, 383, 419, 491 6) palindromic 383
Thank you all very much for these different approaches and the excellent explanation of working.
Teachers' Resources
Why do this problem?
This problem is an accessible context in which pupils can apply their knowledge of number properties and the terminology of position. It provides a great opportunity for learners to reason logically and to communicate their reasoning with others, developing their listening skills.
Possible approach
Introduce the first part of the challenge to the whole group and explain any words which the children are unfamiliar with, going through some examples of palindromes on the board. Give pupils time to work on the first part of this task in pairs. It might be useful to print out copies of it from this sheet (word, pdf). You could bring them together for a mini plenary after a short time, asking whether they can suggest some clues that are not needed and how they know that they are redundant.
Suggest that pairs continue to work on the problem, recording whatever and however they find useful. Let them know that you will be asking them to explain their reasoning, as opposed to simply focusing on the answer.
As you go round the room, listen out for children who are using logical reasoning to eliminate the redundant clues and to find the number. They might well use vocabulary such as 'because' and/or 'if ... then ...'. You could explain to a few pairs that you'd like them to share what they have been saying with the whole group in the plenary.
Bring everyone together again to share their solution but in particular to share examples of logical reasoning that led to it. You can then set the group off on the follow-up challenge where they make or draw the tower from the second part of the question, focusing on explaining their reasoning to their partner.
Key questions
Which clues have you used so far?
Which clues do you have left to use?
Are there any clues that don't tell you any more information?
Can you explain why?
Possible extension
Pupils could be asked to write down or draw their answer, along with a written explanation of their reasoning. They could also think of their own number or tower of blocks and write clues for another group to solve.
Possible support
Using the sheet of clues cut into individual pieces of paper is a good way for each one to be read individually, and they can be grouped according to which children think are the most important and which are giving the same information as another clue.
