That number square
Always, sometimes or never? KS1
Are these statements relating to calculation and properties of shapes always true, sometimes true or never true?
Animated triangles
Jig shapes
Can you each work out what shape you have part of on your card? What will the rest of it look like?
Problem
This challenge is best done in a group of at least four children.

You'll need to print out this sheet or, if you would like much larger cards, these sheets. The sheets will need to be cut into twelve separate cards.
Share all the cards out amongst the group.
Can you each work out what shape or shapes you have part of on your card?
Can you describe the shapes without showing it to anyone else?
What will the rest of the shape or shapes look like do you think?
How could you sort the cards?
We would love to hear your descriptions and hear about the ways you sorted or arranged the cards.
This problem is also available in French, called Casse-tête de formes.
Getting Started
Remember that this activity is designed for you to try in a group so try to persuade some friends or family to join you!
Can you think of a good way of arranging the cards?
Student Solutions
This problem encouraged you to work as a group to discover all of the different shapes on the cards. Part of the challenge was to describe the shapes (or part of them) on your own card and understand the explanation of others. In this way, you could work together to determine all of the different shapes in the Jig Shapes challenge.
Charlie, from The Haberdashers' Aske's Boys' School, suggested that it's good to try to describe the sides and edges that you see on your card. He also suggested describing any whole shapes.
We wonder whether any of you tried arranging the cards? Have a go - what happens?
We also received some photos of the finished problem. Thank you to both Ci Hui Minh Ngoc (who attends Kong Hwa School in Singapore) and Owen (who is home educated in the UK). Owen also recorded the different types of shapes in his solution. We wonder if you can name the shapes too and perhaps suggest some shapes that we might have included? Perhaps you might design your own puzzle for another group to solve, using some of those different shapes?
Here's is Owen's photo of his finished problem:

Teachers' Resources
Why do this problem?
The intention of this problem is that children will work together as a team. It should help in developing mathematical language about shape and position, as well as encouraging learners to listen carefully to others and tweak their own ideas accordingly.
You may like to read our Let's Get Flexible with Geometry article to find out more about developing learners' mathematical flexibility through geometry.
Possible approach
The cards have been designed to join together like a jigsaw so that the picures of the shapes are complete, but it may be better not to tell children this immediately. Instead, invite the group to find a way to organise or sort the cards. At this stage, members of the group can help each other find adjoining cards, but discourage them from simply giving someone else their card. If you are doing the problem as a class activity you could use sticky-tack to fix the cards to the board. Encourage the children to describe the shapes they can see as the whole 'jigsaw' is built up.
Alternatively, you could invite each group to hide two of the cards and challenge them to create the jigsaw without them. Can they draw what they think is on the missing cards? Is there more than one possible solution? Does the position of the missing cards in the jigsaw make a difference to how difficult it is to draw them?
Key questions
Possible extension
Learners who think this activity is trivial have not solved the problem! How can the cards be organised, arranged or ordered? Encourage them to help other members of the team in a cooperative spirit. They can also be challenged to make their own Jig-shape puzzle using all the geometric shapes they can.
Possible support
It may be appropriate for some children to share cards with someone who is more confident with language about shape than they are themselves.
Poly plug rectangles
The computer has made a rectangle and will tell you the number of spots it uses in total. Can you find out where the rectangle is?
Problem
This activity has been inspired by Doug Williams' Poly Plug resource. You can find out more details, including how to order sets of Poly Plug, on the Mathematics Centre website. However, you do not need sets of Poly Plug to have a go at this activity - please see below and take a look at the Teachers' Notes.
In this activity, the monkey secretly makes a rectangle using equal rows of spots on the $5$ by $5$ grid.
The aim is for you to find the rectangle by testing spots on the interactivity below.
Once you think you know where the monkey's rectangle is, click the 'Ready' button.
Which spot is a good one to test first? Why?
If you had to use as few test spots as possible, how would that change the way you play?
Are there some total numbers of spots that are easier than others?
We would love to hear about the strategies you use for finding the monkey's rectangle.
You may be interested in the other problems in our Jaunts into Geometry Feature.
This problem featured in an NRICH video in June 2020.
Getting Started
Student Solutions
Thank you to everybody who sent us their ideas about how to find the monkey's rectangle. You can see some videos of children working on this task in our Early Years Children's Thinking section.
Sion from Twyford School in England sent in this strategy:
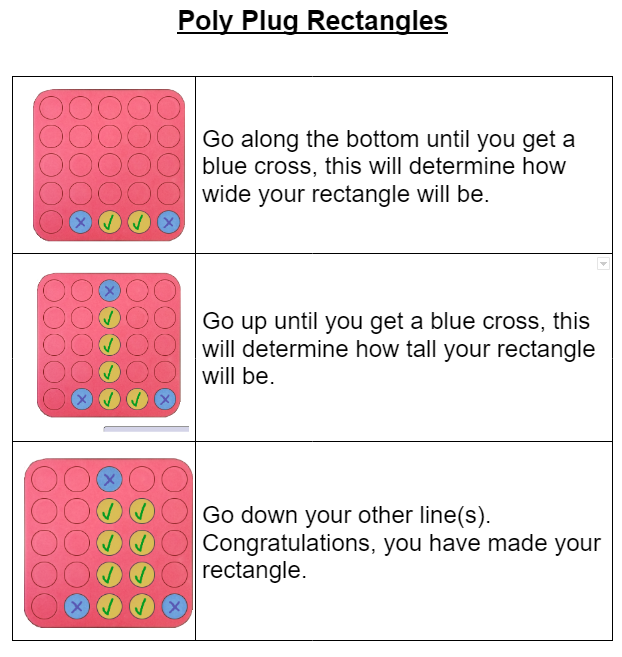
Well done, Sion - I agree that this strategy will always work!
I wonder if there's a way that Sion could change this strategy to use fewer test spots?
Louis from Prospect House School in England sent in this picture of the grid:

Thank you for sending in this picture, Louis. Can you see where the rectangle will be? The rectangle in this grid is actually a special type of rectangle - what other name do we have for rectangles like this one?
If we didn't have the monkey's clue about how many plugs are used in the rectangle, could we still work out exactly where the rectangle will be using Louis's test spots? Why or why not?
We thought you might also like to see these sketches, drawn by a member of the NRICH team as he was working on a new interactivity for this task:
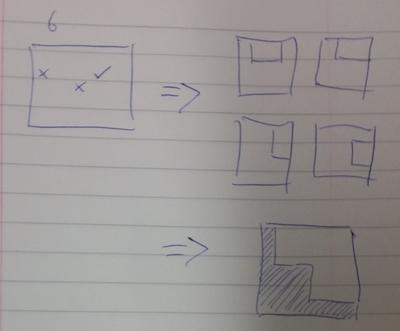
What might he be thinking?
If you would like to get in touch with us about how you approached this task, please email us with your ideas.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Learners could play a version of the game in pairs which allows diagonal rectangles too.
Possible support
Annotated videos
Clip 1 (above): We gave the children some time to play with the Poly Plugs as these were new to them. Not all used them to make patterns within the grid but almost everything was mathematical! There was a lot of noise, most of it productive, and our feeling was that if we hadn't given them this time, they would not have been so focused later on.

Picture 2: Having given them time to play freely, we then suggested they make any pattern or picture they like using just six plugs. We used this child's pattern to draw out the properties of a rectangle.
Clip 3 (above): We then introduced the class to the interactivity. (The interactiivty has since been updated so looks a little different now.) We made the mistake of using a rectangle of four plugs, rather than building on the work they'd just done using six plugs to make a rectangle. You can see the difference in their reactions in this clip and clip 4 which does use six plugs. We re-wrote these teachers' notes after this experience.
Clip 4 (above): In this clip, we encourage the children to find the rectangle more quickly and this time it contains six plugs.
Clip 5(above): We were keen that the children should share their thinking. It was interesting, but unsurprising, that they were disappointed when a plug turned blue.
Clip 6 (above): In this clip, we confronted their keenness to choose only positive examples, trying to help them to see that a blue plug could give them far more information than a yellow one. We're not sure we won though!
Always, sometimes or never?
Are these statements relating to odd and even numbers always true, sometimes true or never true?
Problem
Are the following statements always true, sometimes true or never true?
You could cut out the statement cards and arrange them in this grid.
|
When you add two even numbers together the answer is even |
When you add two odd numbers together the answer is odd |
If you add an even number to an odd number the answer is even |
|
When you multiply by an odd number the answer is odd |
When you multiply by an even number the answer is even |
Doubling a number results in an even number |
|
When you multiply a number by itself the answer is even |
The sum of four even numbers is divisible by four |
Adding three consecutive numbers results in an even number |
Can you find examples or counter-examples for each one?
For the “sometimes” cards, can you explain when they are true? Or rewrite them so that they are always true or never true?
Getting Started
Can you think of an example when it isn't true?
How do you know that it is always true?
Is it possible to check all examples? Is there another way of knowing?
Student Solutions
Well done to everybody who investigated these statements and found examples or counter-examples. We haven't received many solutions to this problem yet, so please email us if you have a solution you'd like to share with us.
Usmaan and Mayeda from Marner Primary School in the UK each sent in a solution for one statement. Mayeda said:
When you add two odd numbers together the sum is an odd number?
I think it's never true because if you find the sum of any odd number together like 23 plus 59 it equals 82 and 82 is an even number not an odd number. Also if you do 97 plus 65 it equals 162 and 162 is even so this means that adding two odd numbers equals an odd number is not true.
Usmaan said:
When you multiply a number by itself the answer is even?
It's sometimes true because if you do 4x4 the product is 16 and if you do 9x9 it's 81 and 81 is an odd number so it's sometimes true.
Good ideas - it's easy to show that a statement is 'sometimes' true when you can find both an example and a counter-example for it! I wonder why adding two odd numbers together never gives an odd number?
Teachers' Resources
Why do this problem?
This task is a great opportunity for learners to use reasoning to decipher mathematical statements. We often make mathematical claims that are only true in certain contexts and it is important for learners to be able to look critically at statements and understand in what situations they apply.
The example here only refers to one key topic but similar statements could be created for any area of maths.
Possible approach
You may want to start with one statement and have a class discussion about whether it is true. Ask learners to think of some examples to illustrate the statement and decide whether it is always, sometimes or never true. If they decide it is sometimes true, they could think about what conditions make it true.
Groups of learners could be given the set of statement cards to sort into the grid sheet. Taking each card in turn they could decide if it is always, sometimes or never true. Then they could justify their reasoning. If they think it is always true or never true, they could explain why they think this is. If they think it is sometimes true they could start by coming up with cases for each and trying to generalise.
For learners who have had more experience of reasoning it might be good to ask them to try and write their ideas down in a clear way, perhaps for just one or two of the statements to start with.
It would be worth sharing ideas as a class at the end. You could pick up on a statement that has been problematic or where there does not seem to be a consensus and support a whole class discussion.
Key questions
Can you think of an example when it isn't true?
How do you know that it is always true?
Is it possible to check all examples? Is there another way of knowing?
Possible extension
Learners could be asked to come up with their own statements for things that are always, sometimes and never true within a topic area. Again they should try to justify their reasons and specify the conditions necessary.
If appropriate, pupils could try the problems Always, Sometimes or Never? Number and Always, Sometimes or Never? Shape which use similar ideas.
Possible support
When discussing as a class, suggest types of numbers to try. Learners often need to start with concrete examples to develop their understanding of a particular concept before they can before they can develop their reasoning within that area. Manipulatives such as Numicon can be useful for building an understanding of the difference between odd and even numbers, and can be used by all learners to support their arguments.
Always, Sometimes or Never? KS1 might be a good starting point for pupils who need more support.
