Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Mr Barton Maths Podcast - Alison and Charlie
Age 11 to 18
Challenge Level 





On 30$^{th}$April 2018, Charlie Gilderdale and Alison Kiddle were interviewed by Craig Barton for his Mr Barton Maths Podcast. On this page, we share the main themes that were discussed, with links to the activities we mentioned, and other useful resources.
NRICH is not just for high attainers
We talked about the challenge level star rating system that we use, from relatively easy (1-star) to very challenging (3-stars), and pointed out that we have many more 1-star and 2-star problems than 3-star problems. Here are some of our favourite 1-star activities which can be used with most Key Stage 3 classes:
Dicey Operations
Add to 200
Dozens
Mixing Lemonade
What's it Worth?
Estimating Angles
Time pressure - how to fit NRICH tasks into a busy curriculum
Sometimes, it might feel like there's too much pressure to get through the curriculum, and NRICH tasks are a luxury that there isn't time to include. We discussed ways that NRICH tasks can actually save you time, by making strong connections between different curriculum areas so that students are revising one topic while meeting another for the first time, or bringing together several different mathematical ideas in one task. Here our some of our favourites (which are all either 1-star or 2-star problems):
M, M and M
Isosceles Triangles
Factors and Multiples Puzzle
Up, Down, Flying Around
Perimeter Expressions
Which is Bigger?
Temperature
The NRICH Pedagogy
Tilted Squares is one of our favourite examples of a task linked to a curriculum topic (Pythagoras' theorem), where students can explore, make conjectures, and generalise. Watch these video clips showing extracts from a lesson of us working on this problem with a group of 14 year old students.
Fluency or Problem Solving - a false dichotomy
We believe that problem solving does not have to be done at the expense of students developing fluency in key mathematical skills. By choosing tasks carefully, teachers can provide opportunities for students to engage in purposeful practice.
Mathematical Etudes - article by Colin Foster
Factors and Multiples Game
Completing Quadrilaterals
Charlie's Delightful Machine
Warmsnug Double Glazing
Pair Products
Cyclic Quadrilaterals
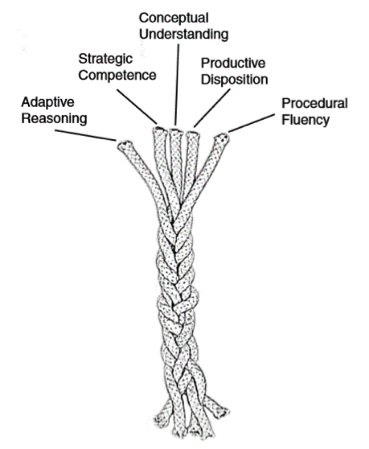
In "Adding It Up" Kilpatrick, Stafford and Findell suggested five essential aspects for developing young mathematicians: conceptual understanding; procedural fluency; strategic competence; adaptive reasoning and productive disposition.
The interwoven and interdependent nature of these five essential aspects are powerfully captured by the image of the rope. Many NRICH problems are written with this model in mind.
Low Threshold High Ceiling tasks to aid with differentiation
We discussed the use of Low Threshold High Ceiling tasks, which offer the opportunity for different groups of students within the same class to work on the same task but reach different end points. Here are some of our favourite Low Threshold High Ceiling tasks.
Summing Consecutive Numbers
Shifting Times Tables
Odds and Evens
Unequal Averages
Marbles in a Box
Hollow Squares and What's Possible?
Finally, here are some of our general resources which we mentioned during the podcast:
What we think and why we think it
Enriching the Secondary Curriculum
Secondary Mapping Document pages
Short Problems

