Which is bigger?
Which is bigger, n+10 or 2n+3? Can you find a good method of answering similar questions?
Problem
Which Is Bigger? printable sheet
You may wish to explore the problem Which Is Cheaper? before working on this task.
Which is bigger, $n+10$, or $2n+3$?
How did you decide?
Here's how I decided:
But then my friend said:
Can you explain why we have come to different conclusions?
Is there a diagram you could draw that would help?
For the following pairs of expressions, can you work out when each expression is bigger?
Here are some challenges to try:
- Find two expressions so that one is bigger whenever $n< 5$ and the other is bigger whenever $n> 5$.
- Find three expressions so that the first is biggest whenever $n< 0$, the second is biggest whenever $n$ is between 0 and 4, and the third is biggest whenever $n> 4$.
- Find three expressions so that the first is biggest whenever $n< 3$, the second is biggest when $n> 3$, and the third is never the biggest.
- Find three expressions so that one of them is the biggest regardless of the value of $n.$
You may also be interested in the other problems in our Many ways to see Feature.
Getting Started
Can you fill in the rest of the table below?
$n$ | $n+10$ | $2n+3$ |
| 4 | 14 | 11 |
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | 20 | 23 |
How else could you represent this information?
Student Solutions
We had lots of solutions to this problem. There are too many to include everyone, but we hope the examples below give you a flavour of how people approached the problem.
Which is bigger, $n+10$ or $2n+3$?
Many students started testing values by substituting values of $n$, including Kabin from Dartford Primary Academy in UK, Maria from Colston's Girls' School in the UK, and the students from Ganit Kreeda, Vichar Vatika in India, who worked on this problem collaboratively. Like these students, several of you recognised that the answer to which expression is bigger depends on $n$. Some solutions arranged their work in a table, which showed how they had worked systematically as they varied the value of $n$. This is Maria's work for integer values of n from 1 to 8:
You may wonder whether testing these values is enough to answer the question. Natalija from St George's British International School in Italy tested values of n from 1 to 10 and noted also that for all larger values of $n$ the second expression will be greater than the first.
Clara from Herlufsholm in Denmark, Archisman from the Future Foundation School in India and Ron, Ata, Jonathan and Mitra from Ashmole Academy sent in this answer, which reflects the results from the tables and also Natalija's idea :
If you substitute $n$ with something smaller than $7$, $n+10$ is smaller.
If you substitute $n$ with $7$, then both $n+10$ and $2n+3$ are equal.
If you substitute $n$ with something bigger than $7$, $2n+3$ is bigger.
Lots of students recognised this result and then set out to prove it. Some used algebra, including the students from Ganit Kreeda, Vichar Vatika. Here is the algebraic argument they produced together:
$n+10=\underline{n+3}+7$ and $2n+3=n+\underline{n+3}$
This clearly shows that $n+10=2n+3$ when $n=7$. Can you see why?
$n+10>2n+3$ when $n<7$.
$n+10 < 2n+3$ when $n>7$.
This is one of several neat ways of working algebraically that were submitted.
Naomi and Justin from Dulwich College Seoul showed how this leads to a cut-off of 7. This is Naomi's work:
If you want $2n+3$ to be bigger than $n+10,$ then your $n+3$ has to be bigger than $10.$ Which means if your $n$ is bigger than $7$, $2n+3$ will be bigger than $n+10$
We wondered how this is the same and how it is different from the method the students from Ganit Kreeda shared.
Adithya from Hymers College in the UK, Yoochan from Dulwich College Seoul and Ana wrote out more of their algebraic reasoning.
$n+10 \gt 2n+3$
then, subtract $n$ from each side:
$10 \gt n+3$
subtract $3$ from each side:
$7 \gt n$
This shows that if $n$ is smaller than $7$, $n+10$ is greater than $2n+3$.
Now, let's look at if $2n+3$ is greater than $n+10.$ Then the equation [inequality] will go:
$2n+3 \gt n+10$
like the previous equation, subtract $n$ from each side:
$n+3 \gt 10$
and subtract $3$:
$n \gt 7$
So, this shows that if n is greater than $7$, $2n+3$ is greater than $n+10$.
You can see another algebraic approach in the work below from Miriam from IEX Maximo Laguna in Spain. Miriam combined algebra with tables and graphs of $y=n+10$ and $y=2n+3$:

Imeth from Pristine Private School in United Arab Emirates, Yatharth from Watford Boys Grammar School, Ci Hui from Queensland Academies for Science Mathematics and Technology in Australia also used graphs in their investigations and arguments. Ci Hui combined tables with graphs using this spreadsheet. Anay from Hymers College in UK also used graphs and annotated this to explain their interpretation.

As Anay explains, both equations are equal at $n=7$. For $n$ less than $7$, $n+10$ will be bigger. This is shown by the graph having larger $y$-values or being 'ahead' of $y=2n+3$ as Anay expresses it. For $n$ greater than $7$, $2n+3$ will be greater than or 'ahead' of $n+10$, so $2n+3$ is bigger.
Yatharth from Watford Boys Grammar School and Leo explained why one expression grows faster than the other. Leo said:
This scenario was created because $n+10$ goes up by $1$ every time you increase the value of $n.$ However $2n+3$ goes up by $2$ every time you increase the value of $n$ (by one).
Yatharth was one of several students who connected this description with the gradients of the two graphs:
$n + 10$ and $2n+3$ both intersect each other at $n = 7$ so before $n = 7$, $n+10$ would be bigger as the gradient is much smaller than $2n+3$. After $n= 7$, again due to gradients , $2n+3$ increases at a faster rate than $n+10$ and is bigger as we go forward.
Which is bigger, $2n+7$ or $4n+11$?
Students tried similar approaches to those above.
Ana from the UAE created this graph:
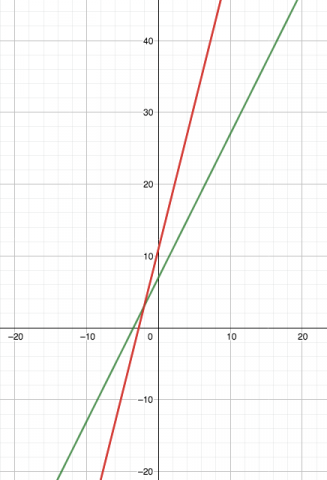
The red line is $y=4x+11$ and the green line is $y=2x+7$
On a graph we can see that the point of intersection is $(-2, 3)$
So when $n\gt -2$ then $4n+11\gt 2n+7$ and when $n\lt -2$ then $4n+11\lt 2n+7$
Abdullah, from Doha College in Qatar, built on his algebraic work from the first part of the problem:
This method also works for other expressions. For instance, when comparing 2n + 7 and 4n + 11, we start with the inequalities 2n + 7 > 4n + 11 and 2n + 7 < 4n + 11. The first inequality simplifies to 7 - 11 > 4n - 2n, which gives -4 > 2n, or n < -2. The second inequality becomes n > -2. At n = -2, both expressions are equal since 2n + 7 = 4n + 11 = 3. So in this case, 2n + 7 is bigger when n < -2, they are equal when n = -2, and 4n + 11 is bigger when n > -2.
Which is bigger, $2(3n+4)$ or $3(2n+4)$?
Yatharth from Watford Boys Grammar School and Ana both used a graphical solution. Here is Ana's graph

The green line is $y=2(3n+4)$ and the red line is $y=3(2n+4).$
As Yatharth explained:
Both these functions have a gradient of 6 and are always parallel as a result so they never intersect. As a result, the one with the highest $y$-intercept would be the greatest for all $n$ and that would be $6n + 12$ opposed to $6n+8$
Yoochan, Justin and Adithya also used algebra. This is Yoochan's work:
Let's first simplify $2(3n+4)$ and $3(2n+4)$ to $6n+8$ and $6n+12$
If $6n+8$ is greater than $6n+12$:
$6n+8 \gt 6n+12$
Divide by $2$:
$3n+4 \gt 3n+6$
Subtract $3n$:
$4 \gt 6$
If $6n+8$ is greater than $6n+12$, we get an equation of $4$ is greater than $6$, which is totally wrong. So, this proves that $6n+8$ cannot be greater than $6n+12$, and $6n+12$ is always greater than $6n+8$, so matter what the value of $n$ is.
Which is bigger, $2(3n+3)$ or $3(2n+2)$?
Clara and Ben said that the expressions are the same. Ben explained why:
I found that with the expressions $3(2n+2)$ and $2(3n+3)$ they always total an equal amount due to the sole fact that you add the number which you multiplied $n$ by. These two numbers are $2$ and $3$. If you've added $2$ you times by $3$ and if you add $3$ you times by $2$ this then leads to an equal amount.
Adithya, Ana, Justin and Yoochan used algebra. This is Yoochan's work:
$2(3n+3)$ and $3(2n+2)$
Let's simplify this to $6n+6$ and $6n+6.$
We can see that these two are equal in value, so no matter what $n$ will be, these two equations have the same output.
Kanav from Sachdeva Public School in India drew out a contrast between this question and the previous one:
There is a constant change in the values.
In case 2(3n+3) and 3(2n+2), all values are the same, and there is a constant change of 6.
In case 2(3n+4) and 3(2n+4), the values are increasing by 6 in both expressions. All values are different.
Find two expressions so that one is bigger whenever $n\lt5$ and the other is bigger whenever $n\gt5.$
Hrishikesh and Isha, both from Ganit Kreeda, Vichar Vatika gave pairs of expressions.
Hrishikesh: $n+8$ and $2n+3$
Isha: $5n+6$ and $4n+11$
Clara gave the expressions: $2n$ and $n+5$
Nathan from British Vietnamese International School suggested: $n+9$ and $2n+4$
Nathan showed this works by substituting different values of $n$.
Adithya explained some reasoning which helps to find the expressions:
To find two expressions that satisfy the above constraints, the two expressions must be equal to each other when $n$ takes a value of $5$.
For example, $n+7$ and $2n+2$ would be two feasible expressions.
A few students started from $x=5$ and worked backwards. As Edward from Woodhey High School in England explains:
To find 2 expressions where one is bigger when n > 5 and the other bigger when n < 5, we start with n > 5. On its own, n and 5 as two individual expressions would satisfy the question, so to make our expressions more complicated, we need to do the same to each side. If we multiply both sides by 3, add 2n and subtract 3, our inequality becomes 5n – 3 > 2n + 12, with 5n – 3 being the greater expression when n > 5
Ana used a similar approach to constructed two expressions which are equal when $n=5$, but started with a graphical interpretation:
The point of intersection of the expressions must be $x=5$. $$\begin{align}x&=5\\
3x&=2x+5\\
18x&=12x+30\end{align}$$
I added $2x$ then multiplied both expressions by $6$ to reach two expressions with an intersection point of $5.$ So when $n\gt 5$ then $18n\gt 12n+30$ and when $n\lt 5$ then $18n\lt 12n+30.$
Siddhant from Singapore International School used this fact:
I took a positive coefficient of $x$ and added it to a constant, to give a larger coefficient of $x.$ This gives us the equation:
$2x + n = 3x$
Now I substituted $x$ to be $5$, as only then would the two [expressions] be equal to each other.
$2(5) + n = 3(5)\\
10 + n = 15\\
n = 5$
Therefore, the two expressions are:
$2x + 5$ and $3x$
I then plotted this on a graph, and inferred that when $x\lt5$, the line $2x+5$ is greater than $3x.$ When $x\gt5$, the line $3x$ is greater than $2x+5$.
Find three expressions so that the first is biggest whenever $n\lt0$, the second is biggest whenever $n$ is between $0$ and $4$, and the third is biggest whenever $n\gt4.$
Clara and Nathan substituted in whole numbers to check that their inequalities worked.
Nathan: $10-n$, $n+\frac{17}2$ and $2n+4$
Clara: $-n$, $n+5$ and $2.1n$
I tried to keep the numbers simple as there is no need to overcomplicate things. However I got the $2.1$ because $2$ worked but eventually there would be two numbers that where the same so $2.1$ was the easiest option to change to. I used excel to help me with this as it did all the sums for me really quickly and it was easy to make small iterations.
I multiplied $n$ by a negative a lot because it meant that as $n$ increased, $-n$ decreased making it easy to use when one formula had to be bigger than the other at only a certain point.
Siddhant and Ana used graphs again. This is Ana's work:

To find three expressions where the first one is the biggest when $n\lt0$, the second one is the biggest when $0\lt n\lt4$ and the third is the biggest when $n\gt4$ the intersections of the first and second line need to be $x=0$ (Point I) and the intersection of the second and third line needs to be $x=4$ (Point J).
With the graph it is visually demonstrated which value is the largest at any value of $n.$
The equation of the first expression (red) is $-n$
The second expression (blue) is $n$
The third expression (orange) is $3n-8$
Adithya used a quadratic expression:
In order to determine an expression which is the biggest when $0\lt n \lt 4$, the expression is set to be equal [when $n$ is equal to] $0$ and $4$. This establishes a quadratic with roots of $n=0$ and $n=4.$ In this case a maximum turning point is requires and so a negative quadratic should be chosen. Therefore, following all the above constraints required for this quadratic expression we establish $-n(n-4)$ which can also be written as $4n-n^2.$
The first expression which must be biggest whenever $n\lt0$ is $-n$ and the third expresion which is the biggest whenever $n\gt4$ is $n-4.$
Justin constructed the expressions algebraically:
Let's start with the expression $n+10$. If this expression is bigger than the second expression whenever $n\lt0,$ then the first and second expressions must be equal when $n=0.$ Let's set the coefficient of the second expression to $2,$ and label the constant $c.$ Then:
$(0)+10=2(0)+c$
$\Rightarrow 10=c$
The second expression is $2n+10.$ We know that $2n+10$ is greater when $n\gt 0$ and $n+10$ is greater when $n\lt0$ and not vice versa through trial and error:
$(1)+10 \lt 2(1)+10$
$\Rightarrow 11<12$
If $2n+10$ is bigger than the third expression whenever $0\lt n \lt 4$, then the second and third expressions must be equal when $n=4.$ Let's set the coefficient of the third expression to $3,$ and label the constant $c.$
$2(4)+10=3(4)+c$
$\Rightarrow 18=12+c$
$\Rightarrow 6=c$
The last expression is $3n+6.$ We know that $3n+6$ is greater when $n\gt4$ and $2n+10$ is greater when $n\lt4$ and not vice versa through trial and error:
$2(5)+10\lt3(5)+6$
\Rightarrow $20\lt 21$
$5\gt4$, $2n+10\lt3n+6$.
$2(3)+10\gt 3(3)+6$
$\Rightarrow 16\gt15$
$3\lt4$, $2n+10\gt3n+6$.
Assuming $n+10$ is the first expression, the three expressions are $n+10$, $2n+10$ and $3n+6$.
Find three expressions so that the first is biggest whenever $n\lt3$, the second is biggest when $n\gt3,$ and the third is never the biggest.
Clara gave this example:
$-n+5$, $n$ and $n-100$
Miriam gave four sets of examples, including one where she generalised the idea:
$n+4$, $2n+1$ and $2n$
$n+7$, $2n+4$ and $2n$
$n+11$, $2n+8$ and $2n$
$n+k$, $2n+k-3$ ($k>0$) and $2n$.
The second and third lines must be parallel.
Adithya and Justin used graphical solutions. Like Miriam suggested, Adithya used parallel lines:
The three expressions would be $-n-3,$ $n+3$ and $n.$
Graphically this produces the following (the blue line represents $-n-3,$ the purple line represents $n+3$ and the black line represents $n$
Justin used a quadratic:

A quadratic graph with a negative coefficient would satisfy the requirement of never being the biggest, as both ends would curve downward. If the quadratic graph is the biggest at one point, we could decrease the constant or move it left/right across the x-axis. In this case, none of this necessary. The graph of $-n^2$ is in green.
Find three expressions so that one of them is the biggest regardless of the value of $n.$
Again, Clara found three which work for whole numbers:
$n^2+5$, $n+4$ and $n+5$
$n^2$ was really useful because it meant that if $n$ was negative $n^2$ would make it positive.
Aakarsh from Ganit Kreeda, Vichar Vatika suggested these expressions:
$n+21$, $n-2$, $n+1$.
$n-2$ is always the smallest number.
Adithya, Ana and Justin all used parallel lines. Can you connect this to Aakarsh's suggestion above? This is Justin's work:
If three lines in a plane are parallel, they will not intersect - the biggest will not change. Lines that are parallel have the same slope. Then, the expression with the highest constant will be biggest.
Since the specific numbers do not matter as long as the coefficients are the same, we can just choose any numbers - let's say $\frac{1}{2}n+2$, $\frac{1}{2}n+4$, and $\frac{1}{2}n+6.$
The graph below shows that $\frac{1}{2}n+6$ is biggest regardless of the value of $n$:

Teachers' Resources
Why do this problem?
This problem highlights the importance of variables in algebraic expressions, and offers opportunities to explore straight line graphs and simple inequalities. By switching between numerical, algebraic and graphical representations, students can gain insights into the effects of changing a variable. The last part of the problem encourages a playful curiosity where students can experiment with graphing software to try to solve each challenge.
Possible approach
Start the lesson by posing the question:
"Which is bigger, $n+10$, or $2n+3$?"
As the expressions are plotted, the class can decide whether they satisfy the requirements. In order to capture the idea that there are infinitely many sets of expressions that satisfy each condition, students could suggest tweaks to the functions that would still satisfy the conditions.
Key questions
Would it help to express the relationship graphically?
Possible support
Possible extension
