Year P16 Being curious

Can you work out which spinners were used to generate the frequency charts?

Charlie likes to go for walks around a square park, while Alison likes to cut across diagonally. Can you find relationships between the vectors they walk along?

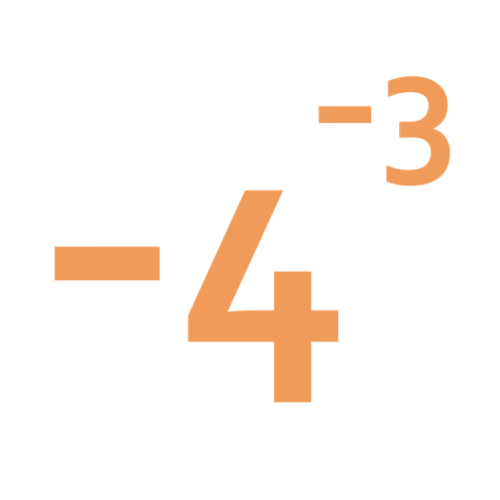
What does this number mean? Which order of 1, 2, 3 and 4 makes the highest value? Which makes the lowest?

There are many different methods to solve this geometrical problem - how many can you find?

Does it make any difference how we write powers of powers? 

Investigate the family of graphs given by the equation x^3+y^3=3axy for different values of the constant a.