Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Hollow Squares



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem offers a historical 'hook' from which some numerical and algebraic discoveries can be made. The starting point of arrangements of soldiers leads to properties of the difference of two squares.
This problem, used in conjunction with What's Possible? and Plus Minus, could offer students insight into the factorisation $a^2-b^2=(a+b)(a-b)$. It is a nice example of a Low Threshold High Ceiling task, as students can move from the initial visual context to more abstract algebraic representations and generalisations. You can read more about
Low Threshold High Ceiling tasks in this article.
Possible approach
You may wish to use these slides to introduce the problem.
"In Napoleonic battles a hollow square was a popular formation for an infantry battalion designed to cope with Cavalry charges." Show the picture of Wellington's army.
Show this image, the second slide.
"Here's a small battalion arranged in a symmetric hollow square. Can you work out how many soldiers there are?"
Talk to your neighbour to check that you agree. Did you work it out the same way?"
Invite students to describe their methods for working out how many soldiers there are in the picture. The two most common methods are to subtract the 4 x 4 square from the 8 x 8 square, or to divide it into four identical 2 x 6 rectangles. Make a record of the methods on the board:
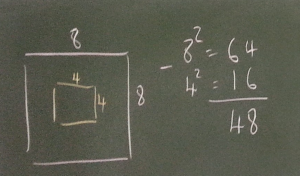
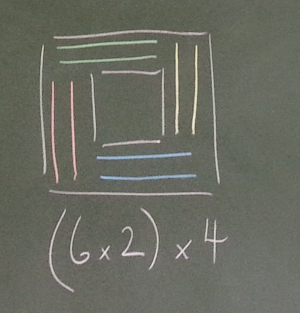
It's really valuable for students to see both methods, so share them if students don't suggest them. See Alison's and Charlie's methods in the problem.
"Sometimes it might be easier to use one method, and sometimes it might be easier to use another. Have a go at working out how many soldiers there are in these images, ideally using both methods."
Show image 2 and image 3 (the next two slides). After students have explained how they calculated the number of soldiers and recorded it, the board might look a bit like this:
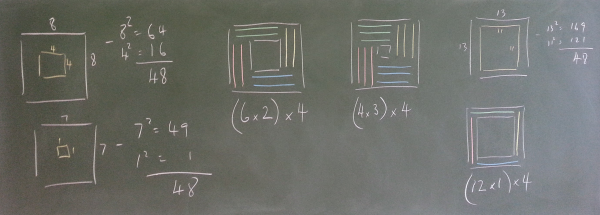
"We now have a way of working out how many soldiers there are in any symmetric hollow square formation."
"But what if we had some soldiers and needed to know how they could be arranged?"
In a while I'm going to challenge you by giving you a number of soldiers. You need to be able to tell me straight away whether they can be arranged in a symmetric hollow square formation, and if so, how many different formations, and the dimensions of the squares."
If students are unsure of how to start with this, suggest that they try some particular cases, for example 60, 72, 120 soldiers.
Bring the class together to discuss their findings. You may wish to invite students to show their working for a particular case. Here's what the board might look like if they have been finding the arrangements for 120 soldiers:
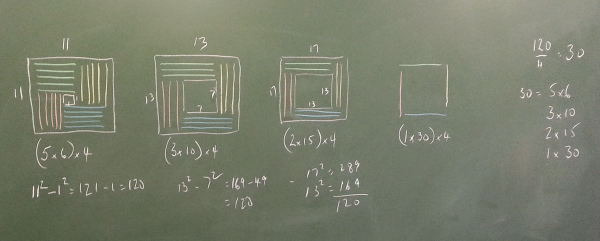
"Now you should be able to quickly work out all the possible formations for any number of soldiers that's a multiple of four."
"Let's try it: if you had 720 soldiers, how many symmetric hollow square arrangements could there be?"
At this stage, students should be able to tackle this without doing any more drawings, and be able to explain there will be nine different arrangements corresponding to the 9 factor pairs of 180.
Finally, if it's not already cropped up, discuss how to work out the dimensions of the two squares from the factor pairs. Students could be invited to construct a table like this:
| Factor Pairs | Hollow Squares |
| $1, 180$ | $181^2-179^2$ |
| $2, 90$ | $92^2-88^2$ |
| $3, 60$ | $63^2-57^2$ |
| $4, 45$ | $49^2-41^2$ |
| $5, 36$ | $41^1-31^2$ |
| $6, 30$ | $36^2-24^2$ |
| $9, 20$ | $29^2-11^2$ |
| $10, 18$ | $28^2-8^2$ |
| $12, 15$ | $27^2-3^2$ |
This is a natural break point if you wish to spread the work over multiple lessons. The 'punchline' of this part of proceedings could be noticing that the sum and difference of the factor pairs gives the two square numbers in the table above, a tantalising teaser of the difference of two squares formula which could emerge in the next lesson.
In a follow up lesson, you could show the final slide or image 4 and image 5. This introduces the idea of asymmetric hollow squares, where the number of soldiers is not necessarily divisible by four.
You may wish to look at the teachers' notes to What's Possible? and Plus Minus for some ideas on how to move students' thinking on to more general understanding of the properties of the difference of two squares.
Key questions
How can we quickly work out how many soldiers there are?
How can we "work backwards" to find all the arrangements of soldiers?
Why is it impossible to arrange some numbers of soldiers in hollow square formation?
Possible support
Offer some more structure initially, by suggesting students work on the different arrangements for 60, 72 and/or 120 soldiers before asking the more challenging question requiring them to find a general method.
Possible extension
Plus Minus offers a proof of the identity for the difference of two square numbers, and some interesting follow-up questions.

