Plus minus
Can you explain the surprising results Jo found when she calculated the difference between square numbers?
Problem
This problem follows on from Hollow Squares and What's Possible?.
Jo has been experimenting with pairs of two-digit numbers. She has been looking at the difference of their squares.
Jo has collected together some answers which she found quite surprising:
$$55^2-45^2=1000$$ $$105^2-95^2=2000$$ $$85^2-65^2=3000$$
Can you find other pairs which give multiples of $1000$? Do you notice anything special about these pairs of numbers?
Jo was also surprised to get these answers:
$$89^2-12^2=7777$$ $$78^2-23^2=5555$$
Can you find any other pairs which give repeated digits? Do you notice anything special about these pairs of numbers?
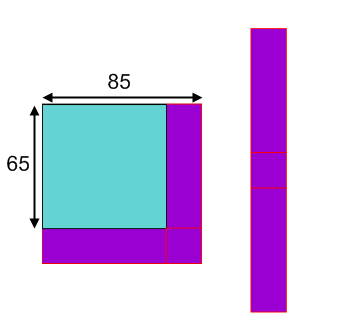
Jo wanted to explain why she was getting these surprising results. She drew some diagrams to help her. Here is the diagram she used to work out $85^2-65^2$:
Now you should be able to work out these calculations without a calculator:
$$7778^2-2223^2$$ $$88889^2-11112^2$$
Can you write $1000, 2000, 3000...$ as the difference of two square numbers?
Can you write any of them in more than one way?
Can you write any repeated-digit number as the difference of two square numbers?
What about numbers like $434343$, $123321$, $123456$...?
Is it possible to write every number as the difference of two square numbers?
This problem is also available in French: Plus ou Moins
Getting Started
Look at the diagram below:

Student Solutions
Tom, from Wilson's School, found some other pairs which gave multiples of 1000 and repeated digits:
Other pairs that give multiples of $1000$ are:
$60^2 - 40^2 = 2000$
$70^2 - 30^2 = 4000$
$75^2 - 25^2 = 5000$
$80^2 - 20^2 = 6000$
$85^2 - 15^2 = 7000$
$90^2 - 10^2 = 8000$
All these pairs add up to 100 which is a factor of 1000.
Other ways to make multiples of $1000$ are $95^2 - 45^2 = 7000$ and $95^2 - 55^2 = 6000$. These numbers when added together become a factor of the answer.
Other pairs that give repeated digit answers are:
$67^2 - 34^2 = 3333$
$56^2 - 45^2 = 1111$
The numbers in the tens columns add together to make 9 while the numbers in the units columns add together to make 11.
Tabitha from The Norwood School, Hannah from Munich International School, Richard from Comberton Village College, and Paul, Dulan and Priyan from Wilson's School all explained how the diagram helped them to work out the difference between two square numbers. Here is Richard's explanation:
By drawing a $85 \times 85$ square and a superimposed $65 \times 65$ square, and subtracting the areas, a strip which covers two lengths of the larger square is formed. When segments of the strip are rotated, a rectangle is formed that has a constant width of the difference of the squares' sides and a length of the sum of the squares' sides.

So the dimensions of the purple rectangle are: width $85 - 65 = 20$, length $85 + 65 = 150$
This implies that the area of the purple strip is equal to that of the rectangle, $20 \times 150 = 3000$.
In general,by drawing a square of length $x$ with a superimposed square of length $y$, the area of the strip will be $(x+y)(x-y)$, so $x^2 - y^2 = (x+y)(x-y)$
James and Nat from Sawston both used this formula for the difference of two squares to help them to find pairs of numbers. Hannah used the formula to work out some of the other things posed in the problem:
$7778^2 - 2223^2 = (7778 - 2223)(7778+2223) = 5555 \times 10001 = 55555555$
$88889^2 - 11112^2 = (88889 - 11112)(88889 + 11112) = 77777 \times 100001 = 7777777777$
Lyman from Nanjing International School showed how the numbers could be made in lots of different ways by finding factors, including some examples using decimals. Here are some ways of making 1000:
$251^2 - 249^2$
$127^2 - 123^2$
$55^2 - 45^2$
$35^2 - 15^2$
$500.5^2 - 499.5^2$
$102.5^2 - 97.5^2$
$66.5^2 - 58.5^2$
$32.5^2 - 7.5^2$
Finally, Richard explained more generally how to make multiples of 1000 and numbers with repeated digits:
Any number of the form $n \times 10^3$ where $n$ is an integer, can be expressed as $x^2-y^2$ when $x + y = 100$ and $x - y = 10n$.
This is not the only case. More generally, it can be formed when $x + y = u \times 10^a$ and $x - y = v \times 10^b$, where $u \times v < 10$ and $a + b = 3$ or where $u \times v$ is equal to some multiple of $10$ and $a + b = 2$.
This is because $x^2 - y^2 = (x+y)(x-y) = uv \times 10^{(a+b)}$.
A repeated number can also be generated quite easily. A number of the form $mm$ can be expressed as $x^2 - y^2$ when $x + y = 11$ and $x - y$ is equal to $m$.
A number of the form $mnmn$ is expressible when $x + y = 101$ and $x - y = mn$.
$mnomno$ is expressible when $x + y$ is equal to $1001$ and $x - y = mno$
Well done to all who submitted solutions.
Teachers' Resources
Why do this problem?
This problem offers students a chance to discover the identity for the difference of two square numbers. They are expected to work as research mathematicians, starting from simple examples, noticing patterns, developing conjectures and explanations that lead to proofs and further exploration.
It recognises the power of diagrams to help us make sense of algebraic generalisations.
Possible approach
This problem follows on from Hollow Squares and/or What's Possible?
Write these first two examples from the problem on the board:
$$65^2-35^2=3000$$
$$55^2-45^2=1000$$
Ask students to suggest other pairs of numbers where the difference of their squares is a multiple of $1000$. Write their suggestions on the board.
If they only offer pairs of numbers that add up to $100$, write up
$$85^2-65^2=3000$$
$$85^2-35^2=6000$$
"Do you notice anything special about these pairs of numbers?"
Encourage students to use anything they notice to generate some more examples.
"Mathematicians are always interested in explaining anything that they notice."
Share this diagram with the class:

The following questions address the key ideas that we want students to encounter. Allow students plenty of time to reflect on these questions, maybe working in pairs initially, and discuss answers as a class:
"What is the connection between this diagram and the calculation $85^2-65^2$?"
"How could we work out the area of the long purple rectangle (without a calculator)?"
"Can you draw similar diagrams for some of our other calculations?"
"How can these diagrams help us to develop a quick method for evaluating $a^2-b^2$ for any values of $a$ and $b$?"
Now introduce students to another set of interesting results:
$$89^2-12^2=7777$$
$$78^2-23^2=5555$$
Can students explain why the digits are repeated, using the insights they have gained earlier?
Can they generate some similar examples?
How about $555555$? $434343$? $505505$?
When appropriate, bring the class together to share and compare strategies.
Finally, set students the task of exploring possibilities for generating "interesting" numbers of their own, to present to the rest of the class at the end.
Possible questions that students might wish to consider:
Can you write $1000, 2000, 3000...$ as the difference of two square numbers?
Can you write any of them in more than one way?
Can you write any repeated-digit number as the difference of two square numbers?
What about numbers like $123321$, $123456$...?
Another exploration that might yield conjectures about differences between square numbers is to look at the areas of rings of different widths. This article explains one student's work on this.
Key questions
How does the diagram represent the difference between two square numbers?
Possible support
Pair Products is a good problem to introduce students to algebraic ways of representing general numerical results.
Possible extension
