These activities focus on finding all solutions. Working in a systematic way will ensure no possibilities are left out.
problem
Favourite
School fair necklaces
Age
5 to 11
Challenge level
How many possible symmetrical necklaces can you find? How do you know you've found them all?
problem
Favourite
Beads and bags
Age
5 to 11
Challenge level
How could you put these three beads into bags? How many different ways can you do it? How could you record what you've done?
problem
Favourite
Half Time
Age
5 to 11
Challenge level
What could the half time scores have been in these Olympic hockey matches?
problem
Favourite
Buying a Balloon
Age
7 to 11
Challenge level
Lolla bought a balloon at the circus. She gave the clown six coins to pay for it. What could Lolla have paid for the balloon?
problem
Favourite
Fifteen cards
Age
7 to 11
Challenge level
Can you use the information to find out which cards I have used?
problem
Cubes Here and There
Age
7 to 11
Challenge level
How many shapes can you build from three red and two green cubes? Can you use what you've found out to predict the number for four red and two green?
problem
Favourite
Trebling
Age
7 to 11
Challenge level
Can you replace the letters with numbers? Is there only one solution in each case?
problem
Favourite
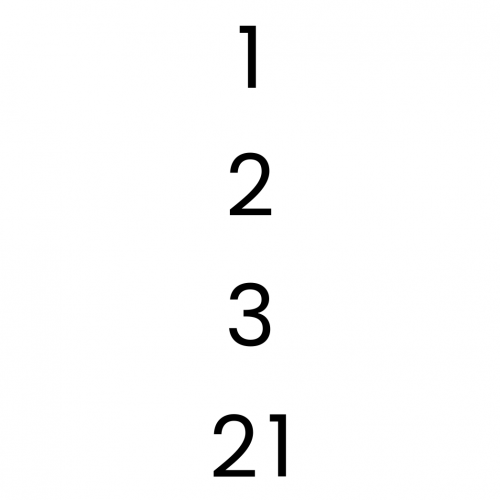
Factor Lines
Age
7 to 14
Challenge level
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.
problem
Favourite
Sealed Solution
Age
7 to 11
Challenge level
Ten cards are put into five envelopes so that there are two cards in each envelope. The sum of the numbers inside it is written on each envelope. What numbers could be inside the envelopes?
problem
Favourite
Magic Vs
Age
7 to 11
Challenge level
Can you put the numbers 1-5 in the V shape so that both 'arms' have the same total?
problem
Favourite
Greater Than or Less Than?
Age
7 to 11
Challenge level
Use the numbers and symbols to make this number sentence correct. How many different ways can you find?
problem
Favourite
All the Digits
Age
7 to 11
Challenge level
This multiplication uses each of the digits 0 - 9 once and once only. Using the information given, can you replace the stars in the calculation with figures?
problem
Favourite
Finding Fifteen
Age
7 to 11
Challenge level
Tim had nine cards each with a different number from 1 to 9 on it. How could he have put them into three piles so that the total in each pile was 15?
problem
Favourite
Button-Up Some More
Age
7 to 11
Challenge level
How many ways can you find to do up all four buttons on my coat? How about if I had five buttons? Six ...?
problem
Favourite
This Pied Piper of Hamelin
Age
7 to 11
Challenge level
Investigate the different numbers of people and rats there could have been if you know how many legs there are altogether!
problem
Favourite
Reach 100
Age
7 to 11
Challenge level
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
problem
Favourite
5 on the clock
Age
7 to 11
Challenge level
On a digital clock showing 24 hour time, over a whole day, how many times does a 5 appear? Is it the same number for a 12 hour clock over a whole day?
problem
Favourite
Nine-Pin Triangles
Age
7 to 11
Challenge level
How many different triangles can you make on a circular pegboard that has nine pegs?
problem
Favourite
Inky Cube
Age
7 to 14
Challenge level
This cube has ink on each face which leaves marks on paper as it is rolled. Can you work out what is on each face and the route it has taken?