Perimeter Possibilities
I'm thinking of a rectangle with an area of 24. What could its perimeter be?
Problem
Perimeter Possibilities printable sheet
Watch the video below.
How many other possible perimeters can you find, for a rectangle with an area of $24\text{cm}^2$?
Now watch the video to see what Alison and Charlie did next.
Here are some questions you might like to consider:
- What other odd number perimeters can you make, if the area is $24\text{cm}^2$?
- What is the smallest perimeter you can make, if the area is $24\text{cm}^2$?
- What about the largest perimeter?
- Which perimeters in between is it possible to make?
More generally...
- Is it possible to make a rectangle with a fractional perimeter but a whole number area?
- Is it possible to make a rectangle with a whole number perimeter but a fractional area?
Take a look at Can They Be Equal? to explore rectangles where the area is numerically equal to the perimeter.
Getting Started
Imagine two islands with an area of $24$, one with dimensions $6$ by $4$ and the other $12$ by $2$.
Which island has more land by the sea shore?
Student Solutions
Many people must have worked really hard on this one, there were lots of detailed answers. Well done! Some people found some solutions like Alison's.
Area: 24 cm2
| Size | Perimeter |
| 4 cm x 6 cm | 20 cm |
| 3 cm x 8 cm | 22 cm |
| 2 cm x 12 cm | 28 cm |
| 1 cm x 24 cm | 50 cm |
A key idea is that you can use fractions or decimals to get more solutions. Alison found one more for us, and Patrick found a few extra too.
| 1.5 cm x 16 cm | 35 cm |
| 0.5 cm x 48 cm | 97 cm |
| 0.25 cm x 96 cm | 192.5 cm |
Notice that we can get an odd number for the perimeter in more than one way, and even find a fractional perimeter. Thomas and Zaki made a great observation.
There are infinitely many perimeters you can make with an area of 24 as you
can keep on multiplying the length by 2 and dividing the width by 2 so the
perimeter keeps getting bigger.
Raadiyah realised that you could divide by numbers other than 2 to find the following.
| 0.000001 cm x 24000000 cm | 48000000.000002 cm |
| 0.0000001 cm x 240000000 cm | 480000000.0000002 cm |
Amy had a great idea for finding a small perimeter using square roots. The square root of 24 is not even expressible as a fraction or a finite decimal, it is irrational!
To get the smallest possible perimeter it needs to be a square so I found the square root of 24 which was approximately 4.898979486.
| $\sqrt{24}$ cm x $\sqrt{24}$ cm | $4\times \sqrt{24}$ cm |
| 4.898979486 cm x 4.898979486cm | 19.59591794 cm |
If you know how to plot tricky graphs and how to find the solution to simultaneous equations you might like to think about how to make any possible perimeter.
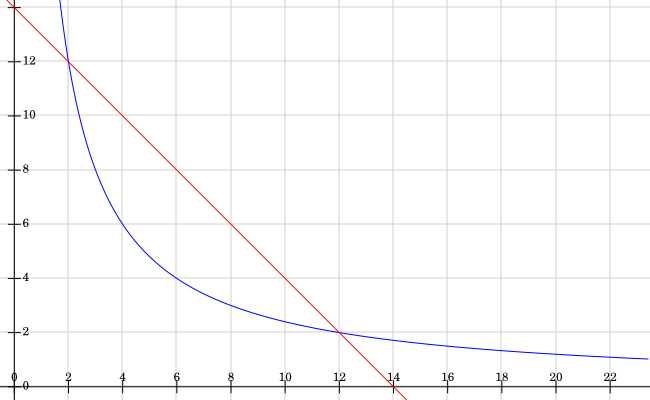
I've plotted the graphs 2x+2y=28 in red and xy=24 in blue. Where do the lines intersect? What does this tell us about the possible rectangles?
Teachers' Resources
Why do this problem?
Many mathematical tasks about area and perimeter focus on the two separately. This problem combines both by inviting students to consider the different possibilities for the perimeter when the area of a rectangle is fixed.
The problem offers opportunities to gain insights that can be applied to a variety of other area and perimeter tasks such as Can They Be Equal?, Changing Areas, Changing Perimeters, Warmsnug Double Glazing, and Fence It.
Possible approach
This printable worksheet may be useful: Perimeter Possibilities.
This problem can lead to many different questions that can be explored in different ways to suit your class. You may wish to watch the two videos in the problem and then introduce the task in a similar way:
"I'm thinking of a rectangle with an area of $24$cm$^2$. What could its perimeter be?"
Students could write their responses on mini-whiteboards. Then, once the class have had time to come up with their answer(s), gather responses on the board in a table like this one:

"Look at the dimensions and perimeters. What do you notice?"
Write on the board any 'noticings' that the students come up with. This might include:
All the perimeters are even
The perimeters are getting larger
The sum of the dimensions is equal to half the perimeter
The dimensions are all factor pairs of $24$
As the perimeter gets larger the rectangle gets 'narrower'/'skinnier'/'thinner'.
After some discussion: "Actually, the rectangle I was thinking of had an area of $24$cm$^2$ and a perimeter of $35$cm. Can you use your insights to work out the dimensions of my rectangle?" Allow time for a proper discussion about developing a strategy to solve the problem using the students' initial insights.
"In pairs, I would like each of you to think of a rectangle, work out its area and perimeter, and then give this information to your partner to see if they can work out the dimensions of your rectangle.
Do this a few times and keep a record of your rectangles and the methods you are using.
To start with, stick with rectangles whose area and perimeter you can work out in your head."
This is a really good opportunity for students to use trial and improvement. Although there are algebraic methods, trial and improvement allows students to use their insights to get to the answer quite quickly and efficiently.
The lesson could be rounded off by offering students a challenge such as "I'm thinking of a rectangle whose perimeter is $21$ and whose area is $20$. What are the dimensions of my rectangle?"
Key questions
Are the perimeters of rectangles always even?
Why do the rectangles get thinner as the perimeter gets larger? (for a fixed area)
Possible support
Students could be asked to consider rectangles with a fixed perimeter before moving on to rectangles with a fixed area.
Possible extension
Here are some possible follow-up questions:
- What other odd number perimeters can you make, if the area is $24$cm$^2$?
- What is the smallest perimeter you can make, if the area is $24$cm$^2$? What about the largest perimeter?
- Which perimeters in between is it possible to make?
More generally...
- Is it possible to make a rectangle with a fractional perimeter but a whole number area?
- Is it possible to make a rectangle with a whole number perimeter but a fractional area?
Can They Be Equal?, Changing Areas, Changing Perimeters, Warmsnug Double Glazing, and Fence It could be tackled next.
