Copyright © University of Cambridge. All rights reserved.
'Overlap' printed from https://nrich.maths.org/
Show menu
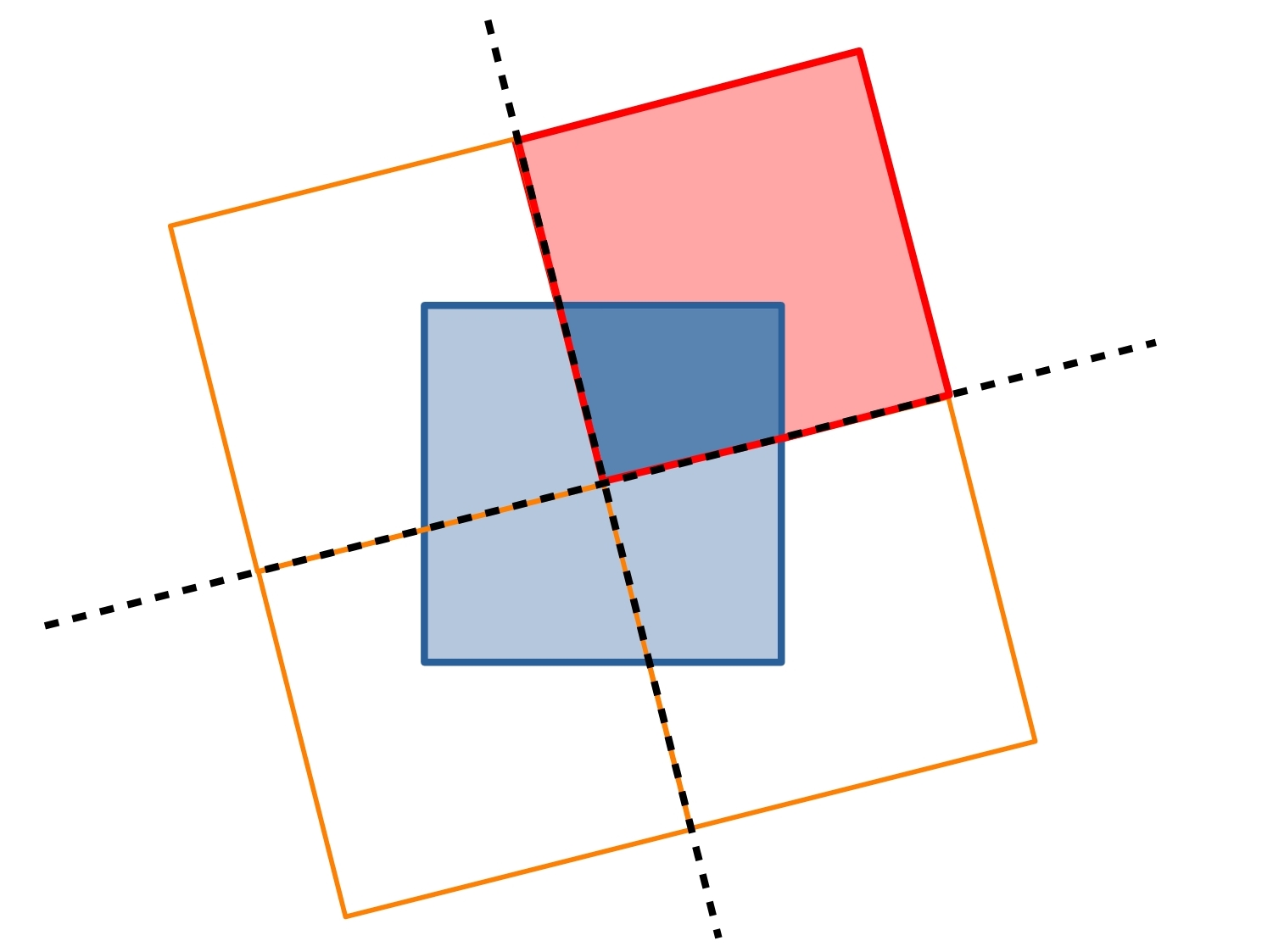
A red square and a blue square of the same size are overlapping so that the corner of the red square rests on the centre of the blue square. Try using the slider to see how the overlap changes as the red square rotates.
Can you show that, whatever the orientation of the red square, it covers a quarter of the blue square?
Here are some ideas that you can use to help you do this:
This picture shows what happens if you rotate the red square by $90^{\circ}$, $180^{\circ}$ and $270^{\circ}$ around the centre of the blue square.
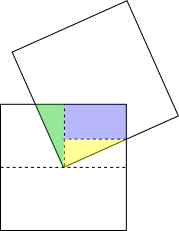
Can you use congurent triangles to complete this proof?

Can you use congruent triangles again to find a different proof?
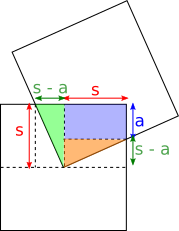
In this method, let each side of the blue square have length $2s$.
Can you use this diagram, and the areas of rectangles and triangles, to find a fourth proof?
If the red square is smaller than the blue square what is the smallest length its side can have for your proof to remain true?