Two Squared
Problem
If you double the sides of a square, the area becomes four times the size. It is quadrupled.
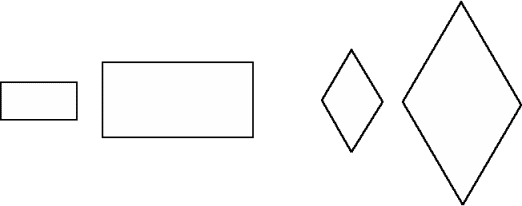
We can try the same thing with a rectangle and a rhombus.
How do the four smaller ones fit into the larger one?
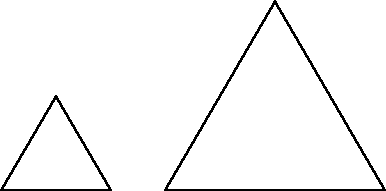
We can then try with equilateral triangles:
And "L" shapes:
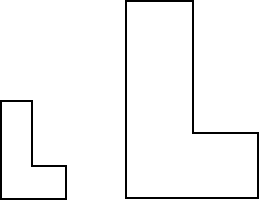
What has to be done to make these fit?
We could try with other shapes like hexagons.
These have to be cut and rearranged.
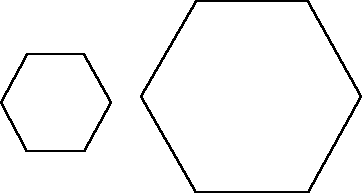
What is the least number of cuts needed to fit four hexagons into one larger hexagon with sides double the length?
Getting Started
You could draw the shapes on squared paper or isometric paper and cut out the smaller ones to fit into the larger ones.
Or you could print these sheets and cut out the shapes.
Don't forget you can rotate the smaller shapes!
TwoSquared 1.docTwoSquared 2.doc
Student Solutions
Cameron from Quenn of the Apostles School sent in the following;
Everything can be done, as hard as it may seem, except for the hexagon.
When I couldn't figure it out I asked my mum and she said that my answer was the best.
You will need to use three half cut hexagons and one full one.
You put the full hexagon in the centre, next you put two halves at the bottom making sure they fit, do the same to the top, next put the last two halves at the sides. See how there are still gaps? This is not possible without more hexagons.
We had separate solutions sent in from Fulham Cross Girls' School from the following pupils, Tianah, Iania, Hagar, Alaa, Rachea, and Jessica. Here are two of them:
Firstly, with your first shape, in your head or on a piece of paper build up your shape e.g four squars as a cube. Then see if it matches with your big shape and count how much shapes there was in your shape your big shape.
I think that you put the the small square inside the big square in any of the corners that's two squared. If you put the small rectangle in the top/bottom left/right corner that's two squared too.
Well done ALL of you!
Teachers' Resources
Two Squared
If you double the sides of a square, the area becomes four times the size. It is quadrupled.
We can try the same thing with a rectangle and a rhombus.
How do the four smaller ones fit into the larger one?
We can then try with equilateral triangles:
And "L" shapes:
What has to be done to make these fit?
We could try with other shapes like hexagons.
These have to be cut and rearranged.
What is the least number of cuts needed to fit four hexagons into one larger hexagon with sides double the length?
Why do this problem?
This problem helps learners to come to terms with the concept of area and also to explore the properties of many straight-sided shapes. It requires some quite difficult visualisation when more complex shapes are used. However, the beginning is very accessible so everyone can become involved quickly.
Possible approach
Some of the later shapes require considerable manipulation to fit in the four smaller shapes. The hexagons are likely to prove the first real difficulty and children will reach different solutions. They may need to count little triangles on the isometric paper to be convinced that they have actually fitted four hexagons into the larger one. Possibly the simplest solution is to cut one hexagon into three rhombi and fit all together like this:
If many learners are having difficulties, the diagram above could be drawn on the board. Isometric paper can be very useful at this point.
At the end, with the whole group together, some solutions and sketches could be discussed. You may want to draw out the fact that doubling the sides of the shape has resulted in four times the area, not double the area. With very visual work such as this some children show unexpected talent and others, who usually succeed at once, have blocks. This means that it is specially helpful if later the children have a few minutes to jot down their feelings.
How did you feel if you got stuck?
What or who helped you?
How did you feel when you cracked the problem?