Sticky data
Problem
This activity is designed to be worked on in a large group or as a whole class. For more information, please read the Teachers' Notes.
Everyone in your group or class will need a sticky note. Write your name on it. You could even draw a picture of yourself on it too.
You'll also need some large sheets of flipchart paper or you could work on the board or the floor.
Draw two long lines on the paper/board/floor, something like this (you might ask an adult to do this for you):
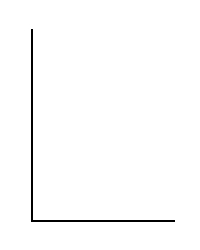
You're going to use your sticky notes and the lines to help find out the answers to some questions. Here are some questions to start you off:
- How many boys and how many girls are there in your group?
- Which month has the most birthdays for your group?
- How old are the children in your group?
We would love to see photos of the block diagrams you create and to know how you went about making them. Could you give a name to the lines in each case?
You will have questions of your own as well. We would like to hear about the questions you asked and to see the block diagrams you made to help answer them.
Getting Started
What other questions would you like to ask?
Don't forget to name the lines of your picture.
Student Solutions
Children from South Darley CE Primary School collected 'sticky data'. They sent these photos:
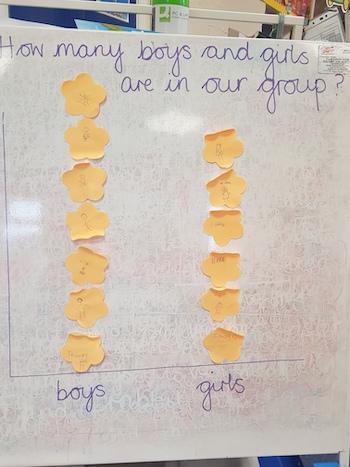
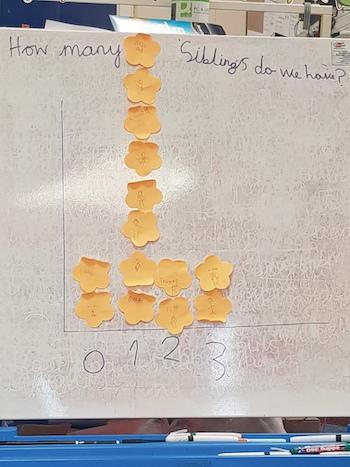
Nicholas wrote about what they did:
We got our sticky notes and then we had to write our name (and picture) and then we had to stick it to the whiteboard.
There is one more boy and also there are 7 boys and 6 girls, and we also did how many siblings we have altogether - 18.
Thank you South Darley!
We also had a good response from Priorslee Primary Academy. Here are their submissions:
Emie, Amran and Jessica wrote:
How many boys and girls are there? There are 16 boys and 13 girls.
Which month has the most birthdays in your group? February, August and October
How old are the children in your group? 10 and 9
Niamh, Manieka, Lydia and Priya wrote:
Firstly, we counted the amount of children in the class and found out that there are 17 boys and 13 girls (not including the teacher). This makes 30 children and one teacher (31 people).
The next thing to do was to ask all the children in the class (including the teacher) what month they were born in, and how old they were. We also asked our teacher what month she was born in and her age.
The next thing we did was we wrote all of the months in the year and the number of children in that month on squared paper. We got three people in January, February, March, April, August and September. In May and July we found that there was one person in each month. In November there was no one, in December there were two people, in June there were four people and
finally with the most people was October with five people (including our teacher Mrs Johnston).
We also found out that nearly all the class are 10. There are 25 people that are 10, and 5 people that are 9.
Marley and Arjan wrote
We worked in a group of two and got post-it notes and asked the entire class for their name and the month they were born in. Once we got the answer, we put it in a bar chart to answer the questions.
1.9-10
2. October
3. 16 boys 13 girls
How many people were born in each Month.
Jan 3; Feb 4; Mar3; Apr 3; May3; Jun3; Jul1; Aug2; Sep1; Oct0; Nov0; Dec1
Amran, Emie and Jessica wrote:
We worked as a group of three but did the whole class. We gave each member of the class a sticky note and asked them to write their name and the month they were born. We then calculated each answer to the following questions that were given. Then we sorted each answer into a graph. Here is part of what we found out:
January: 2 girls and 1 boy
February: 1 girl and 3 boys
March: 1 girl and 2 boys
April: 0 girls and 2 boys
May: 1 girl and 0 boys
June: 2 girls and 1 boy
July: 1 girl and 0 boy
August: 2 girls and 2 boys
September: 2 girls and 0 boys
October: 1 girls and 3 boys
November: 0 girls and 0 boys
December: 0 girls and 2 boys
We then calculated each person's age and how many girls were a certain age and how many boys were a certain age.
3 girls are 9
10 girls are 10
14 boys are 10
2 boys are 9
Libby, Jada-Mia, Neha and Fatima sent in a graph showing their birthdays
Thanks to all of you at Priorslee
From Tiger Class via their teacher at Alexandra Primary School we were sent
My Year 3 class got stuck into Sticky Data today. We created a bar chart to answer the question:
How many girls and boys are there in Tiger Class? We could see clearly, when we had finished, that there were 16 girls and 11 boys in class that day. 
Then we discussed what else we could show using our 'sticky' bar charts. We decided on:
Which month do the Tiger Class children have their birthdays? We had great fun making the bar chart and we had a good discussion afterwards. The children told me that I hadn't labelled it correctly as I hadn't left enough room for all the months on the X-axis. This made it difficult to read. We also hadn't left any room between the bars which also made it
more difficult to read.
At the end of the lesson, we had a good discussion about why we use bar charts and how they make it easier to show information quickly in a way that we understand.
We'd love to see what other bar charts children have created!
Thank you all, we've collected quite a few examples of your sticky data, but keep sending your ideas in!
Teachers' Resources
Sticky Data
This activity is designed to be worked on in a large group or as a whole class. For more information, please read the Teachers' Notes.
Everyone in your group or class will need a sticky note. Write your name on it. You could even draw a picture of yourself on it too.
You'll also need some large sheets of flipchart paper or you could work on the board or the floor.
Draw two long lines on the paper/board/floor, something like this (you might ask an adult to do this for you):
You're going to use your sticky notes and the lines to help find out the answers to some questions. Here are some questions to start you off:
- How many boys and how many girls are there in your group?
- Which month has the most birthdays for your group?
- How old are the children in your group?
We would love to see photos of the bar charts you create and to know how you went about making them. Could you give a name to the lines in each case?
You will have questions of your own as well. We'd like to hear about the questions you asked and to see the bar charts you made to help answer them.
Why do this problem?
Possible approach
You could begin this activity using the children themselves to create a block graph. Pose a question for the class to answer. A good one to start with would be "how could we show how many girls and boys there are in our class?".
Take ideas and if not already suggested, sit or stand the children in two lines. Which line is the longer?
Ask another question, for example, "how could we show how many children have school dinners and how many don't?".
Again after suggestions, sit or stand the children in two lines and talk about what they notice.
Now give each child a sticky note and ask them to write their name on it and decorate it in some way, should they wish.
How could we use the sticky notes to answer the same questions? Give learners time to have a think themselves, then talk to a partner, then share with the whole group (think - pair - share). Some may suggest sorting or grouping the sticky notes on opposite sides of the board, which you could try to begin with. The disadvantage of this method is that it's not so easy to compare the number of boys with the number of girls (unless of course there is a large difference between the two numbers!). Ask the class how the sticky notes could be arranged to make the counting easier. At this point, some may suggest lining the sticky notes up in two rows or two columns, just as they had been doing at the beginning of the activity. You could then superimpose the axes of the block graph as a way of framing the picture, and invite children to suggest labels for each axis. If your class is familiar with block graphs, you could draw the axes on the board right from the beginning.
Having had a go at one block graph all together, you could encourage the children to answer the other questions posed in the problem. They will also have their own ideas. Bear in mind that learners may find it easier to display qualitative data (such as boy/girl as above, birthday months) as opposed to quantitative data (such as number of siblings, number of pets, height) against the number
of children. This is because when showing quantitative data, labelling the axes can be more tricky. This might be the case particularly with continuous data (those that use a scale, such as height) rather than discrete data (such as number of pets). However, try not to discourage children from posing questions involving quantitative data. Instead, listen to their
discussions as they work out what to do.
You may be able to address the above issues to some extent in a plenary by asking the whole group which question they found most difficult to display and why.
Key questions
Possible extension
Possible support