Using Rich Tasks in an Objective Led Culture

Article | Printable page |

Article by NRICH team
Stage: 2, 3 and 4

What were we trying to achieve?


As teachers, we appreciate the need to have clear objectives at the start of lessons but have been aware of the limitations this sometimes seems to place on our ability to get the most out of using rich tasks. Through our case study we tried to address two issues:
  • Objectives that are seen as a strait-jacket, restricting the teachers' room for manoeuvre. These can be a barrier to teachers responding appropriately to the students they are working with, not allowing them to 'go with the flow' of a lesson.
  • Objectives that are solely about content and do not recognise the mathematical process skills that we want students to develop.

How were we trying to achieve our aims?


In our schools we have been working towards creating a balance of content and process-led objectives, moving away from an ethos of just having formal, explicit, content-based objectives at the start of each lesson. Raising the status of process objectives has allowed teachers to be more flexible in their view of what students might achieve in each lesson.

In our planning, we have:

At School A


A team of teachers were planning a new KS3 Scheme of work. They have grouped content objectives into topics and incorporated process objectives that take into account the different teaching approaches being adopted. In any lesson both process and content objectives can be shared with the pupils. NRICH tasks are one of the vehicles through which these process objectives are being introduced. Fortnightly meetings are being used to discuss the outcomes of recent lessons based on NRICH tasks, and to plan future lessons.

At School B


At this school they were happy with the basic structure and content of their existing KS3 Scheme of Work so have adapted it in line with the new curriculum with a focus on processes. They initially looked at algebra units with the intention of replacing various activities with rich tasks. Teachers trialled tasks from the NRICH website to help them decide which ones were most appropriate for their developing Scheme of Work and to identify process objectives they might focus on when using the task. Initially the department had a day off timetable to discuss approaches and begin work on the adjustments. They continued this work in their own time and during department meetings. As they taught the algebra unit they made further refinements. They are planning to move on to the geometry and measure units next.

At School C


This department also started by working on the algebra topics in their KS3 Scheme of Work.
They used rich tasks in a variety of ways. For example, they chose:
For each unit of work the department included key processes in their plans, wrote a 'story' of how each lesson might be taught and completed a mapping diagram of all the processes the students might use. These could then be included in lesson objectives. They continue to work on other units.

At School D


This school made minimal changes to their Scheme of Work but they identified rich tasks and planned for flexibility by using process objectives. This encouraged flexibility because teachers felt they were not being strait-jacketed by a specific content outcome. Students working on the problem Number Pyramids (http://nrich.maths.org/numberpyramids) took the problem in their own direction and wanted to know how to multiply negative numbers and decimals. The fact that students were taking the initiative reflected an important mathematical process that the school was trying to foster.

At School E


The school worked on a longer term project, covering several lessons, focussing on trigonometry content objectives. A small team planned the series of lessons with objectives spanning the sequence of lessons rather than individual lessons. These objectives covered
  • process skills, such as representing and communicating
  • mathematics content
  • links to some of the historical background to measurement and measuring instruments
  • links to real life applications of trigonometry, such as fire engine ladders.
Part of the project also included linking with the Technology department to make clinometers for use in practical activities.

How well are we doing it?


Reflecting the aims of the new curriculum, schools wanted students to focus more often on how they achieved their solutions to problems. This meant that at the start of lessons teachers sometimes gave objectives which consisted solely of process objectives or a combination of process and content objectives. On occasions content objectives were 'held back' for later discussion.

Process and content objectives

NRICH tasks have been used successfully by schools to consolidate knowledge. In these circumstances schools often felt that it was good to give students both process and content objectives at the start of a lesson or sequence of lessons. They felt there was no tension in sharing what was to be learnt and reflecting on this in lesson plenaries.

The NRICH task Diagonal Sums (http://nrich.maths.org/diagonalsums) was included in the first Algebra unit of the Scheme of Work. It introduced students to the merits of using algebra when making generalisations whilst requiring them to engage with the key processes of exploration and conjecturing.

The NRICH tasks Number Pyramids (http://nrich.maths.org/numberpyramids) and More Number Pyramids (http://nrich.maths.org/morenumberpyramids) were used to consolidate work on solving equations and to give students a context in which to construct their own equations and communicate their ideas.

Number Pyramids

Choose three single-digit numbers and write them in the bottom row of the pyramid.

Link to interactive applet
Screenshot of pyramid applet (3 levels)

Try a few more times with different sets of three numbers until you understand what is happening.

Link to interactive applet

Screenshot of pyramid applet (4 levels)

Using the same starter numbers $2$, $1$, $4$ and $6$, rearrange them to find the largest and smallest possible totals at the top of the pyramid.

Can you get these totals in different ways?
Keep a record of the arrangements of the starting numbers which generate each total.
What do you notice about these arrangements?

Test out your observations and insights with other sets of four numbers.
You could include big numbers, small numbers, negatives and decimals.

Can you explain what is happening? Can you explain why it is happening? Can you explain it algebraically?

Adapt your ideas to apply to taller pyramids.


When introducing new ideas however, it was felt that giving content objectives at the start would sometimes pre-empt the journey students would make and not allow them to independently 'notice' the new mathematics on the way. In these cases, the content lesson objectives were sometimes kept general.

For example, when the problem 'Tilted Squares' was used to introduce Pythagoras' Theorem, the Lesson Objective shared with the students referred to area, rather than Pythagoras' Theorem. The project also involved linking to historical background including the work of Pythagoras and the Pythagoreans, and these historical objectives were shared.

Another approach when introducing new ideas, or encouraging students to make connections between different aspects of mathematics, was to 'hold back' content objectives until the end of the lesson or sequence of lessons. Teachers asked students to think about the content objectives in the plenary, once the lesson activity was completed. This encouraged students to reflect on their own learning and think about what they had learned, rather than what they were told they had learned. This approach also supported the teachers involved in assessing pupils' progress.

The Teachers' Notes for NRICH tasks on the website contain useful guidance on content and process objectives, key questions and possible approaches that can be used in the classroom. Teachers have found these very useful.
See, for example, the Teachers' Notes for
Consecutive Numbers (http://nrich.maths.org/consecutivenumbers)
Cuboid Challenge (http://nrich.maths.org/cuboidchallenge)

At School A, NRICH tasks were used to introduce new content in a way that developed students' process skills. For example

In lessons where new mathematics was being developed, or mathematical connections were being made, teachers felt that giving content objectives spoilt the discovery. Teachers focussed initially on process objectives, sharing and agreeing content objectives at the end of the sequence of lessons.

Odds and Evens

There are some sets of coloured balls with numbers on them:

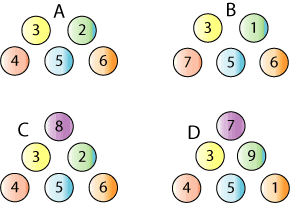
Four sets of coloured balls

A set is mixed up and two balls taken at random. For example:

one ball numbered 4 and one ball numbered 5
The numbers on the balls are added together: $4 + 5 = 9$

The aim is to get as many even numbered totals as possible.
Which set is most likely to give you even totals?

Can you number five balls so that you have an even chance of winning?
How about four balls?
How about six balls?
How about...?

Process objectives


At one school, the department chose to use a school-wide one-off event on the theme of 'conflict resolution' to work as a whole department on two rich tasks. Two problems from the NRICH website were selected for the potential they offered for challenging students to work effectively in groups and to arrive at a shared understanding that could be communicated to the rest of the class. It was these process skills that formed the objectives for the sessions and that were referred to throughout the lesson

The two selected tasks were Zin Obelisk (http://nrich.maths.org/zin) and the slightly more demanding Doesn't Add Up (http://nrich.maths.org/doesntaddup).

In a different school, a lesson on averages had the objective 'to be able to listen to and communicate findings within a group setting'. In this lesson the teacher made it explicit that she was focusing on how the groups worked and discussed amongst themselves rather than on the content outcomes.

This process objective was also used with another group, together with a content objective, 'to be able to calculate averages'. See M, M and M:

M, M and M

There are five positive whole numbers with the following properties:

  • Mean = 4
  • Median = 3
  • Mode = 3

How many different sets of five numbers can you find that satisfy these conditions? Can you convince us you have found them all?

If I also tell you that the range is 10, can you identify my numbers?

Another five positive whole numbers have the following properties:

  • Mean = 31
  • Median = 33
  • Mode = 34
  • Range = 8

How many different sets of five numbers can you find that fit these criteria?

Can you convince us you have found them all?


Lesson objectives are now being used in creative ways which support the teaching and learning of students. Including process objectives has improved the quality and range of mathematical discussions in our classrooms.

This article is the result of the collaborative work of:
Susanne Mallett, Steve Wren, Mark Dawes and colleagues from Comberton Village College
Amy Blinco, Brett Haines and colleagues from Gable Hall School
Jenny Everton, Ellen Morgan and colleagues from Longsands Community College
Craig Barton, Debbie Breen, Geraldine Ellison and colleagues from The Range School
Danny Burgess, Jim Stavrou and colleagues from Sawston Village College
Catherine Carr$\acute{e}$, Fran Watson and colleagues from Sharnbrook Upper School
David Cherry, Chris Hawkins, Maria Stapenhill-Hunt and colleagues from The Thomas Deacon Academy
Charlie Gilderdale, Alison Kiddle and Jennifer Piggott from the NRICH Project, Cambridge

For similar articles about teachers using NRICH go here.
search engine page

Published .