Diagonal Sums

Here is a $100$ square with some of the numbers shaded:


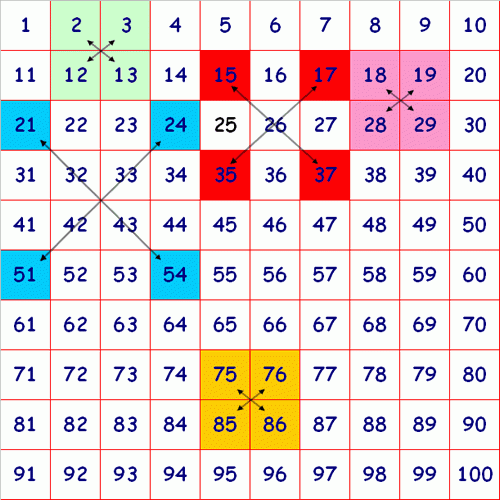
Look at the green square which contains the numbers $2, 3, 12$ and $13$.
What is the sum of the numbers that are diagonally opposite each other?
Do you notice anything?
Look at the pink square.
Does the same thing happen?
What about the yellow square?
You could try with other squares which have four numbers in them.
Why does this happen?

Look at the squares shaded red. They form the corners of a large $3$ by $3$ square.
If you add the numbers diagonally opposite each other, what happens?
Why?

What happens for squares of different sizes?

You may like to print off this 100 square to try out some different squares of numbers.