You can use these printouts of the equations, the graphs without axes , the graphs with axes and the processes to create a card sorting activity.

Scientific processes involving two variables can often be represented using equations and line graphs.

In this problem, $9$ processes, their equations and graphs have been mixed up and shown below. In each case, the two variables are represented by the letters $x$ and $y$ and the labels from the axes of the graphs have been removed.

Which can you match up? What is the interpretation of the variables $x$ and $y$ in each case?

Can you identify the physical interpretation of three key points on each of the graphs?

Processes

1. Number of rapidly dividing bacteria present in a food-limited environment, starting from a small initial sample.
2. Concentration in the blood of a drug following an injection.
3. Angle of oscillation of a real pendulum of length $1$m in air.
4. Volume (litres) against pressure (atmospheres) for $1$ mole of an ideal gas at $0^\circ$ C.
5. Vertical distance travelled by a small, heavy ball dropped from a plane.
6. Rate of reaction of a catalysed reaction in terms of the concentration of reagent.
7. Number of rapidly dividing bacteria present in a food-rich environment, starting from a small initial sample.
8. Hours of daylight per day in a town in the far northern hemisphere.
9. Model of the distance of the Earth from the sun in astronomical units.

Line Graphs

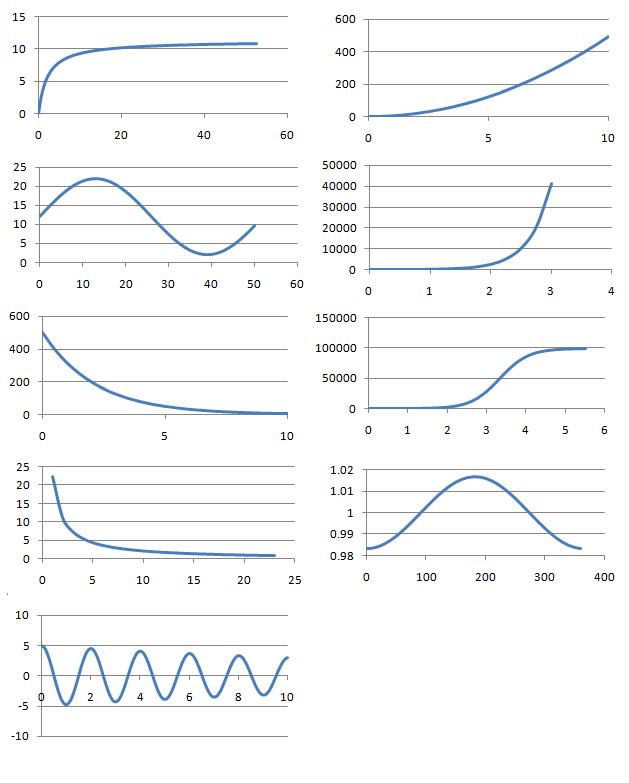
Equations

A: $y(x) = 4.9 x^2$

B: $y(x) =500 \times 2^{-0.6667x}$

C: $y(x) =1- 0.01671\cos(0.0172 x)$

D: $y(x) = 12+10\sin(0.121 x)$

E: $y(x) = 5\cos(3.13 x)e^{-0.05x}$

F: $y(x) = \dfrac{11.3 x}{2.1+x}$

G: $y(x) =10 \times 2^{4x}$

H: $y(x) = \dfrac{1000000}{10+(100000-10)2^{-4x}}$

I: $y(x)x = 22.4133$

The numbers have been carefully chosen to represent certain time/length/unit scales for particular physical phenomena. Can you deduce the reason for the choice of any of the numbers?