Tet-Trouble
Problem
Is it possible for a tetrahedron to have edges of lengths 10, 20, 25, 45, 50 and 60 units?
Can you write a set of general rules for someone else to use to check whether a given six lengths could form the edges of a tetrahedron?
Getting Started
You could cut up some straws to the equivalent lengths and try this for real.
Alternatively, how about drawing some nets and cutting them out to test them?
Student Solutions
The following solution was sent in by Becki from the Mount School, York. Becki uses The Triangle Inequality. Andy from the Garden International School used the same method .
It is definitely impossible to have a tetrahedron which has edge lengths of 10, 20, 30, 40, 50 and 60 units.
This is because to produce a triangle two sides have to be bigger (when added together) than the third. So this tetrahedron won't work because the 10 is too small to make a triangle. e.g. 10, 20, 30
- 20 + 30 > 10 (OK)
- 10 + 30 > 20 (OK)
- but 10 + 20 = 30 so the triangle becomes a straight line.
10 will not go with any other two numbers in the above list.
However it is possible to make a tetrahedron which has lengths 10, 20, 25, 45, 50 and 60 units. The reason is that the numbers are big and small enough to fit the rule of triangles (the sum of two sides bigger than the third) Here is my net of this tetrahedron to explain my answer (not to scale!)
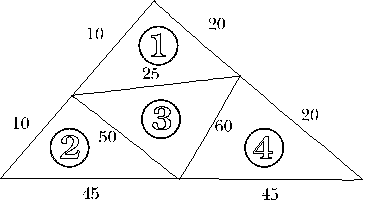
| Triangle 1 | 10 + 25 > 20 | Triangle 2 | 10 + 50 > 45 | |
| 10 + 20 > 25 | 10 + 45 > 50 | |||
| 20 + 25 > 10 | 50 + 45 > 10 | |||
| Triangle 3 | 50 + 60 > 25 | Triangle 4 | 60 + 45 > 20 | |
| 25 + 60 > 50 | 20 + 60 > 45 | |||
| 25 + 50 > 60 | 20 + 45 > 60 |
So all four faces are fine, so it can make a tetrahedron.
Teachers' Resources
Why do this problem?
This problem offers an excellent opportunity for students to practise visualisation and apply an idea normally only used in 2D geometry to a 3D case. Learners will have to consider carefully how to communicate their methods for testing combinations and that they have considered all possibilities.
Possible approach
This printable worksheet may be useful: Tet Trouble.
In silence, write three lengths on the board (for example 3 units, 6 units, 7units) and accurately draw a triangle with sides of corresponding lengths. You could use a dynamic geometry package to do this.
Do it again with three more lengths.
And again but instead of drawing the triangle put a question mark. After some thinking time, encourage a member of the group to come up and draw the triangle.
Finally, list three lengths that will not work followed by a question mark and after time has been taken to realise the impossibility, discuss why this is the case as a group.
Now pose the problem.
Working in small groups the challenge will be to employ systematic approaches as well as applying the triangle inequality.
Take opportunities to pull together different ideas for recording, including the use of nets and working systematically.
Key questions
- How do you know you have tried all possibilities?
- Is it possible to construct more than one tetrahedron?
- Can you find six lengths which will give more than one tetrahedron?
Possible support
Use construction straws of equivalent lengths to make (or fail to make) triangles and tetrahedra.
Possible extension
The problem Triangles to Tetrahedra requires students to work systematically to generate all possible tetrahedra from four particular triangles.
Or there is the problem : Sliced . This is a challenging next step in this kind of visualisation.