Fractions Jigsaw
A jigsaw where pieces only go together if the fractions are equivalent.
Problem
Fractions Jigsaw printable worksheet
You will need to download and print out this jigsaw (or draw the pieces on squared paper), and cut up the pieces into squares (don't cut along the diagonal lines!).
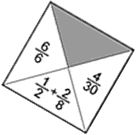
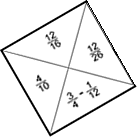
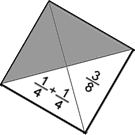
Now try to put the square pieces together without rotating any of them (so that in the finished jigsaw all the numbers are the right way up).
Two pieces may only go next to each other if the edges that touch contain fractions that are equivalent.
Getting Started
Count the number of pieces in the puzzle.
What will the dimensions of the finished jigsaw be?
Some people find it easiest to complete the edges first.
Student Solutions
A Maths Focus Group from Reigate Priory School wrote up the strategy they used to complete the jigsaw:
First we found the corners, which were pretty easy as they had to have $2$ black triangles.
Then we did the edges which have $1$ black triangle but we found that we had $4$ spare, $1$ from each edge.
We realised that these probably had to go together in the middle of the jigsaw, ie: with black triangles touching.
We then worked out the 'inner' corners, ie: the squares that had to have $2$ triangles matching, and then we worked out the squares that had to join these up.
After that there was only $1$ piece left to fit in the middle!!
Jamie from Great Sankey High School described his strategy:
I looked at matching pairs first, and then tried to match them up into a group.
I then saw a pattern and worked from that to complete the jigsaw.
George and Sophie from Hoyle Court Primary in Baildon, Shipley, West Yorkshire started off finding the more obvious equivalent fractions, and formed small sections of the jig-saw. Then they realised they could start to piece sections together. Eventually they recognised the pattern of the triangles around the edge. Their solution is below. Well done to both of them.

Teachers' Resources
Why do this problem:
This problem provides an opportunity to find equivalent fractions and carry out some simple additions and subtractions of fractions in a context that may challenge and motivate students.
For some students this will also invite questions like:
How has this puzzle been created, and how much freedom is there in this structure?
Possible approach :
Give the jigsaw to pairs of students to complete, being ready for discussion that may follow about fractions or puzzles of this type.
Here is a blank outline of the jigsaw for students to create their own, harder/easier versions of the puzzle.
You can create, print out, save and exchange customised jigsaws, domino activities and a variety of rectangular card sort activities using "Formulator Tarsia", free software available from the Hermitech Laboratory website .
Key questions :
- How did you start with this puzzle?
- At what stage did it get hard?
- How did you get through that block?
- How could it be made harder?
Possible support :
Use the blank template and create a jigsaw using only simple fractions. Give some of the piece positions at the start. Get the group creating appropriate jigsaws for each other to try. There may be good discussions in what makes one puzzle harder than another.
Possible extension :
- Can a set of pieces solve in more than one way ?
- How does our answer to these questions change for different size jigsaws.
