Four-triangle arrangements
How many different shapes can you make by putting four right-
angled isosceles triangles together?
Problem
Well, equilateral triangles are great fun to play around with (try Triangle Animals if you haven't already!) but let's not forget the right-angled triangle - particularly the kind that comes from cutting a square in half through a diagonal.
We could take 4 of these and have something like this:
Image
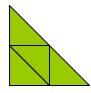
So we can make some rules about how we can re-arrange these four triangles.
Here's a usual rule - EACH SIDE MUST MATCH UP TO A SIDE THAT'S JUST THE SAME LENGTH AND THEY MUST HAVE THEIR VERTICES TOUCHING.
Image

Image
Image

Image

The four arrangments above would obey the rule. But the next two would NOT obey the rule. Can you say a reason why?
Image

Image
So, using plastic, paper, card or other triangles, what arrangements can you make with four right-angled isosceles triangles like the ones at the start?
You will have to decide about allowing "flipping over" or not.
Like in so many investigations it's good after a while to change a bit of the rule and start again.
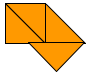
So let's say that the four must be joined together BUT you can have them joining with one vertex and all OR part of a side touching.
For example the red and orange ones we've already seen above are now allowed:
Image

Image

Others might be:
Image

Image

Image
Now it's your turn.
What arrangements can you find with these new rules?
Getting Started
Starting with good squares and getting them cut in half from corner to corner as best as you can is really helpful. If necessary get someone to help.
You can record these by simply drawing around them, but find whatever suits you best. A digital camera may be good - or even a computer drawing program.
How will you know when you have got them all?
Student Solutions
These are the ones we found for the first rule.
Image
Image

Image

Image

Image

Image

Image

Image

Image
Image
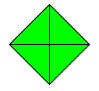
Image
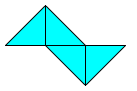
Image

Image
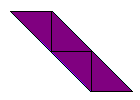
Image
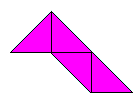
These are some extra ones we found for the second:
Image

Image

Image

Image

Image

Image
Image

Image

Image

Image
Again we worked in a system just moving one triangle and keeping the other three fixed. So there are many, many more to find for this second rule.
