Tables Without Tens
Problem
You will need a piece of squared paper for this activity. If you don't have any, you can get a sheet here.
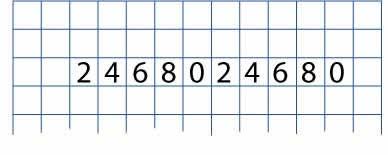
Write the ones digits of the numbers in the two times table from $1 \times 2$ up to $10 \times 2$ in a line. Leave some room at the top of the paper, and some space to the left and right, a bit like this:

Getting Started
Try looking along rows, up and down columns and perhaps along diagonals for patterns in the digits.
When you're finding repeats, you might want to imagine extending the rows to 11 lots of the number, 12 lots, 13 lots... etc.
When you're trying to explain the patterns, don't forget how you've made each row in the first place!
Student Solutions
Those who submitted solutions found that there are many different and interesting patterns to be found in this problem. In addition, some tried to find explanations for these patterns, which was great. As well as being fun, this problem should also help with learning the times tables, as a student from Devagiri CMI Public School, Calicut in Kerala, India found out.
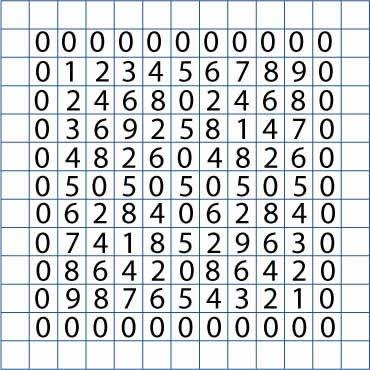
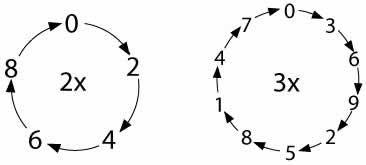
Firstly, let's look at the symmetrical patterns that a few of you found in the tables.
The numbers along the diagonals of the full, completed square show a pattern, as these people discovered: Katie from Sir Jonathan North CC, Isabel and Eleanor from The Manor Prep, Veronika, Miriam, Albin, Carolien and Erin from the Independent Bonn International School, Nitya Andrew and Sydney from Ysgol Pen Y Bryn School in Wales, and a student from Devagiri CMI Public School, Calicut.
Katie found that the diagonal lines follow the rule of symmetry. Isabel and Eleanor described this:
Nitya, Andrew and Sydney mentioned the pattern using numbers to illustrate:
In the right top corner the diagonal downwards numbers (i.e. from top right to bottom left) are $0, 9, 6, 1, 4$ and on the left hand bottom corners the diagonal upwards numbers are also $0, 9, 6, 1, 4$. It is as if the numbers are reflected in a mirror.Veronika, Miriam, Albin, Carolien and Erin from the Independent Bonn International School noticed "symmetry" with the rows for three and seven. They pointed out:
Looking at the sevens, we found out that the numbers were the same as the threes in reverse.The student from Devagiri CMI Public School also found this.
A few people also found a symmetrical pattern when loooking at the five times tables. Here, the only digits in the table are $5$ and $0$. These numbers form a cross-like pattern, running vertically and horizontally through the middle of the table. The repetition of "$5$" and "$0$" should help with remembering the five times tables: the "member of the table" always ends with either a $5$ or $0$ and these alternate. Also, it can show you quickly if a number can be divided by five with no remainder: if this is true, the number must end in a "$5$" or "$0$".
Sam from the Orchard Community Primary School looked at patterns along the columns and rows:
The same pattern occurs from the same digit on both the rows and the columns.For example, look at the sequence of numbers for the two times table, starting in the second row from number two: $2, 4, 6, 8, 0, 2, 4, 6, 8, 0$. Now look at the third column, starting from number two. This is the same: $2, 4, 6, 8, 0, 2, 4, 6, 8, 0$. This is the same if you start from the number three, or four, or five ...
A student from North Walsham Junior School found this too, as did Nitya, Andrew and Sydney from Ysgol Pen Y Bryn.
Luke from Tudhoe Grange found another pattern, but this time it is along the edges of the square. He discovered that in the first column and the last column (ignoring the columns of zeros), there are all of the numbers from $0$ to $9$. Furthermore, the numbers are in order: the sequence increases by one unit going down on the left hand side, and decreases by one unit when going down the right hand side. The same is seen for the first and last rows (ignoring the rows of zeros).
James from Thornton Dales and James from Tudhoe Grange found a similar sort of pattern. James from Tudhoe Grange describes this:
The end result shows that the numbers go up in the first column in $1$s then the next column in $2$s and so on. The pattern continues on to $10$s.Francesca and Katie went on to explain:
The patterns occur because all you are doing is timesing the number of the first column by the number of whichever number of row you want to create the numbers for e.g if you want to find the number for the second column in the third row you would times three by two equalling six because you times the row by the column. By this method you can create the whole table.Some people found patterns when looking at odd and even numbers in the table. For example, George from Summerswood Primary found that the first line (for the one times table) has alternating odd and even numbers, whilst the second line has all even numbers. For the three times table, the numbers are alternating odd and even and for the four times table, all numbers are even. This pattern repeats itself ...
A student from Devagiri CMI Public School also noticed this. He explains:
In the Tables of Even numbers, the ones are always even, while in the Tables of Odd numbers, alternate ones are odd and even.He noticed this general rule: when multiplying two odd numbers, the ones are always odd. You only get an even number if you multiply by an even number. So, to get an even number for an answer, an even number must be involved in the multiplication.
Using this rule he reasoned:
In the times tables of even numbers all the answers are even numbers, because an even number is always involved. In the times tables of odd numbers, only half the answers are odd numbers and the other half even numbers. This is because you only multiply the odd number by an even number half of the time.As we have seen, we can find patterns just by looking at the numbers in the tables. Also, we can try to find further patterns by adding, subtracting, multiplying and dividing various sets of numbers.
Luke from Tudhow Grange and a student from Devagiri CMI Public School looked at patterns found when adding numbers. The student from India found complements of ten in the table (complements are numbers that go together in some way). He noticed:
For each of the times tables, the ones place starts with its own respective number and ends with its complement of $10$. For example, let us consider the one times table. This table starts with $1$, and ends in $9$, and $1+9= 10$. So, $1$ and $9$ are complements of ten. This pattern extends further.Let's stay with the one times table. The second number in the row ($2$ for the one times table) and the second last in the sequence ($8$) are complements in $10$ since $2+8=10$. This is true for the third and third last numbers ($3+7=10$). This is also the case for the fourth and fourth last numbers ($4+6=10$). For the fifth number, you add it to itself ($5+5=10$).
This pattern is seen for all of the times tables. Try this for yourself, by looking along the rows of the different times tables. Now look at the columns. Do you see the same complements of tens?
Teachers' Resources
Why do this problem?
This problem involves learners noticing patterns, and making and proving conjectures. It is, incidentally, also an engaging way of revising multiplication tables! In addition, it is also very useful for encouraging learners to predict what they think they will find out.
Possible approach
You could introduce the investigation by inviting the class to help you record the ones digits of the two times table on the board. You may like to pause with just that row of digits written up, and invite learners to comment on anything they notice. Can they explain the pattern of digits?
Complete the ones digits of the three times table in a similar way, directly underneath the two times table, so that learners get a feel for the task. Encourage them to work in pairs from there so that they are able to talk through their ideas with a partner. Have plenty of squared and plain paper available. (Squared paper can be found here.)
Once they have completed the ones digits of the four and five times tables, draw everyone together again and ask whether they notice any patterns. Invite them to talk to a partner about their noticings, and then encourage everyone to share them with the whole group. Say that mathematicians aren't satisfied with noticing patterns, although that is a great start, we want to know why the patterns occur. Set the class off again, inviting them to choose a pattern they have noticed and try to explain why it occurs.
As they work in pairs, listen out for those children who are drawing on what they know about the number system to explain a noticing. You could warn a few pairs that you'd like them to share their explanations with the whole class in the final plenary.
If you are able, you could extend this task further to look at the zero, one, six, seven, eight, nine and tens times tables, as is suggested.
Key questions
Possible support
Some learners will find it helpful to use a standard $10 \times 10$ 'table-square' to help with the tables. The resulting ones-numbers can then be transferred to a plain sheet of squared paper. This ready-made sheet might help.
