Building Tetrahedra
Can you make a tetrahedron whose faces all have the same perimeter?
Problem
Imagine a tetrahedron made up of four triangles which have the same perimeter.
What might it look like?
Image
You could start to explore by choosing a triangle with a perimeter of 20, say, and use it as the base of your tetrahedron.
Can you find possibilities for the other three triangles if they all have perimeter 20 too?
Of course, if the triangles are all congruent, the perimeters will definitely be equal!
Can you find an example where the triangles aren't all congruent? Can you prove it?
Click below to see a diagram that might help:
Image
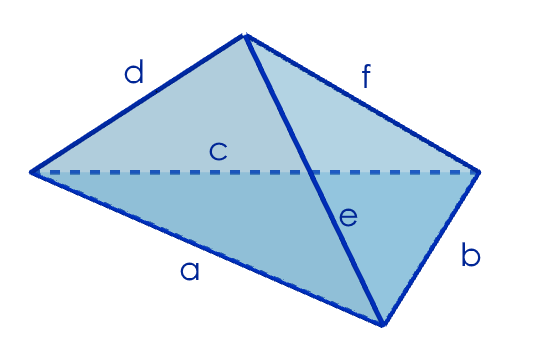
Can you write down expressions for the different perimeters?
What can you deduce if you know these perimeters are all equal?
Can you make a tetrahedron out of any set of four congruent triangles?
Getting Started
Imagine putting together two triangles with a perimeter of 20, edge to edge.
Can you now add a third triangle with the same perimeter?
And a fourth?
Student Solutions
Sam from Bishop Strachan School in Canada used diagrams to show that the the triangles which are the faces of the tetrahedron must be congruent. Click here to see Sam's work, which also shows how it is possible to make a tetrahedron with any 4 congruent triangles.
Agathiyan from Hymers College used algebra to look for tetrahedra whose faces had perimeters of 20:

First of all, I tried and got several possibilities of tetrahedra made out of four triangles with a perimeter of 20.The interesting thing was that I couldn't find a solution that doesn't use 4 congruent triangles. All my solutions had two sides of the same length. Using symbols on
the provided diagram:
Agathiyan from Hymers College used algebra to look for tetrahedra whose faces had perimeters of 20:
Image

$a=f$
$b=d$
$c=e$
And therefore I set out to prove that it is always like this. The first thing I did was add up all the sides of the triangles, so we could get $a+b+c+d+e+f=x:$
$(a+b+c)+(a+d+e)+(b+e+f)+(c+d+f)=20+20+20+20$
$2a+2b+2c+2d+2e+2f=80$
$a+b+c+d+e+f=40$
And since $a+b+c=20$
$d+e+f=20$
Using the equations of other triangles' perimeters:
$d+e+f-(a+d+e)=20-20$ (since $a+d+e$ is the perimeter of one of the faces so must be equal to $20$)
$\Rightarrow f-a=0$
$\Rightarrow a=f$
$d+e+f-(b+e+f)=20-20$
$\Rightarrow d-b =0$
$\Rightarrow b=d$
$d+e+f-(c+d+f)=20-20$
$\Rightarrow e-c =0$
$\Rightarrow c=e$
Using these values and substituting them into the triangles:
$(a+b+c)+(a+d+e)+(b+e+f)+(c+d+f)=80$
$(a+b+c)+(a+b+c)+(b+c+a)+(c+b+a)=80$
Showing all triangles must be congruent. Also it must form a tetrahedron with the triangles sharing the same perimeter, since because they are all congruent, they share a perimeter and also the same sides, therefore all sides should perfectly tessellate in 3D, meaning the tetrahedron can be formed.
$b=d$
$c=e$
And therefore I set out to prove that it is always like this. The first thing I did was add up all the sides of the triangles, so we could get $a+b+c+d+e+f=x:$
$(a+b+c)+(a+d+e)+(b+e+f)+(c+d+f)=20+20+20+20$
$2a+2b+2c+2d+2e+2f=80$
$a+b+c+d+e+f=40$
And since $a+b+c=20$
$d+e+f=20$
Using the equations of other triangles' perimeters:
$d+e+f-(a+d+e)=20-20$ (since $a+d+e$ is the perimeter of one of the faces so must be equal to $20$)
$\Rightarrow f-a=0$
$\Rightarrow a=f$
$d+e+f-(b+e+f)=20-20$
$\Rightarrow d-b =0$
$\Rightarrow b=d$
$d+e+f-(c+d+f)=20-20$
$\Rightarrow e-c =0$
$\Rightarrow c=e$
Using these values and substituting them into the triangles:
$(a+b+c)+(a+d+e)+(b+e+f)+(c+d+f)=80$
$(a+b+c)+(a+b+c)+(b+c+a)+(c+b+a)=80$
Showing all triangles must be congruent. Also it must form a tetrahedron with the triangles sharing the same perimeter, since because they are all congruent, they share a perimeter and also the same sides, therefore all sides should perfectly tessellate in 3D, meaning the tetrahedron can be formed.
Makalp from MGIS in India and David from Singapore both looked for tetrahedra whose faces had perimeter $k$, beginning with the equations
$$\begin{align}a+b+c&=k&(1)\\
a+d+e&=k&(2)\\
b+e+f&=k&(3)\\
c+d+f&=k&(4)\end{align}$$
David used exactly the same method as Agathiyan, and the algebra is exactly the same, except that all of the $20$ s are replaced with $k$ s. This gives the exact same result that all of the triangles must be congruent. Makalp's proof is slightly different:
Subtracting equations from each other to elimate a variable and then rearranging gives the following 6 equations:
$$\begin{align}b+c&=d+e&(1-2)\\
a+d&=b+f&(2-3)\\
b+e&=c+d&(3-4)\\
a+c&=e+f&(1-3)&(A)\\
a+b&=d+f&(1-4)&(B)\\
a+e&=c+f&(2-4)\end{align}$$ Subtracting $(B)$ from $(A)$ to eliminate $f$ gives $$\begin{align}a+c&=e+f&(A)\\
a+b&=d+f&(B)\\
c-b&=e-d&(A-B)\end{align}$$ When this is added to equation $(1-2)$
$$\begin{align}b+c&=d+e &(1-2)\\
+\hspace{2mm}-b+c&=-d+e &(A-B)\\
2c&=2e &((1-2)+(A-B))\end{align}$$
Therefore $c=e$.
Similarly by using the above deduced result and the equations, relationships for $a$, $b$, $d$ and $f$ were also determined.
$a=f,$ $b=d$ and $c=e$
Therefore, there are infinite possible tetrahedrons whose all 4 triangular sides have the same perimeter. All dimensions that follow the above mentioned condition is a possible solution i.e. $a=f,$ $b=d$ and $c=e.$ This, the triangular sides can be equilateral, isosceles and scalene.
$$\begin{align}a+b+c&=k&(1)\\
a+d+e&=k&(2)\\
b+e+f&=k&(3)\\
c+d+f&=k&(4)\end{align}$$
David used exactly the same method as Agathiyan, and the algebra is exactly the same, except that all of the $20$ s are replaced with $k$ s. This gives the exact same result that all of the triangles must be congruent. Makalp's proof is slightly different:
Subtracting equations from each other to elimate a variable and then rearranging gives the following 6 equations:
$$\begin{align}b+c&=d+e&(1-2)\\
a+d&=b+f&(2-3)\\
b+e&=c+d&(3-4)\\
a+c&=e+f&(1-3)&(A)\\
a+b&=d+f&(1-4)&(B)\\
a+e&=c+f&(2-4)\end{align}$$ Subtracting $(B)$ from $(A)$ to eliminate $f$ gives $$\begin{align}a+c&=e+f&(A)\\
a+b&=d+f&(B)\\
c-b&=e-d&(A-B)\end{align}$$ When this is added to equation $(1-2)$
$$\begin{align}b+c&=d+e &(1-2)\\
+\hspace{2mm}-b+c&=-d+e &(A-B)\\
2c&=2e &((1-2)+(A-B))\end{align}$$
Therefore $c=e$.
Similarly by using the above deduced result and the equations, relationships for $a$, $b$, $d$ and $f$ were also determined.
$a=f,$ $b=d$ and $c=e$
Therefore, there are infinite possible tetrahedrons whose all 4 triangular sides have the same perimeter. All dimensions that follow the above mentioned condition is a possible solution i.e. $a=f,$ $b=d$ and $c=e.$ This, the triangular sides can be equilateral, isosceles and scalene.
Teachers' Resources
Why do this problem?
This problem invites students to explore the properties of 3D shapes, and in particular, tetrahedra.Possible approach
The challenge is for students to create a non-regular tetrahedron where all four of the triangular faces have the same perimeter (you could specify a particular perimeter such as 20cm). Students could work with nets and sketches or alternatively create 3D models of tetrahedra in order to explore the constraints on the triangles that make up a tetrahedron, and how that is affected by the additional constraint that the triangles have the same perimeter.Once students come to the conclusion that all of their examples have four congruent triangles, invite them to come up with convincing arguments leading to a proof that it is impossible for the triangles to have the same perimeter unless they are congruent.
Key questions
Imagine putting together two triangles with a perimeter of 20, edge to edge.Can you now add a third triangle with the same perimeter?
And a fourth?
