Fred the Class Robot
Problem
Billy's school has a paved area at the front:
Billy's class had a robot called Fred who could draw with chalk held underneath him.

Billy's teacher drew lines and numbers on the paved area in front of the school so that they could tell Fred where to go.
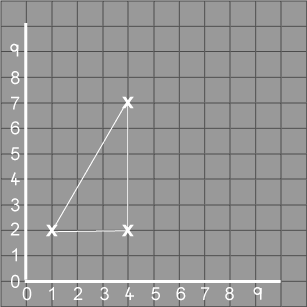
Billy's teacher put a little cross on the point $(1, 2)$ and the children put Fred on the cross. Fred moved to $(4, 7)$, then to $(4, 2)$ and then back to $(1, 2 )$. Fred's chalk drew a line to show where he had been.
Getting Started
Have you counted the number of sides of each shape and looked at the angles? You might like to move your paper around to help you see what each shape is.
Student Solutions
Thank you to Amber from CCHS and two groups of children from Moorfield Junior School (Helen, Katie, Amy and Pauline were one group and the second consisted of Luke, Vicky and Alex) who correctly answered the first parts of the problem. Luke, Vicky and Alex said:
The first shape that Tom drew was a square.The shape that Vicky drew was an irregular pentagon.
Billy also made Fred draw a square.
Amber went on to explain:
We know it is a square and not just any diamond/rhombus because it has four right angles whereas any other kind of diamond/rhombus would have two acute angles and two obtuse angles.Pupils from Mrs Simmons Class at Aqueduct Primary School sent in a wonderful solution to the final part of the question. They say:
We cut squares out, firstly small squares, $1$ square wide, then $2$ squares wide and so on. Then we put the corner of a square onto ($7,4$) and marked the points out. We did this for every size until we could not find any more coordinates that would fit.We found a pattern forming and so we coloured in the squares in lots of different colours and layered them onto the grid.
We then listed all the coordinates we had found on a separate piece of paper. We have named each square a letter, to correspond with the list of coordinates.
They sent the following images to show their solutions:

They also sent the coordinates which Fred would have to go to in order to draw all the squares:
A $( 7 , 4 ) ( 7, 3 ) ( 6 , 3 ) ( 6 , 4 ) ( 7 , 4 )$B $( 7 , 4 ) ( 6, 4 ) ( 6 , 5 ) ( 7 , 5 ) ( 7 , 4 )$
C $( 7 , 4 ) ( 7, 5 ) ( 8 , 5 ) ( 8 , 4 ) ( 7 , 4 )$
D $( 7 , 4 ) ( 8 , 4 ) ( 8 , 3 ) ( 7 , 3 ) ( 7 , 4 )$
E $( 7 , 4 ) ( 7, 6 ) ( 9, 6 ) ( 9 ,4 ) ( 7 , 4 )$
F $( 7 , 4 ) ( 6, 4 ) ( 6 , 5 ) ( 7 , 5 ) ( 7 , 4 )$
G $( 7 , 4 ) ( 9, 4 ) ( 9 , 2 ) ( 7 , 2 ) ( 7 , 4 )$
H $( 7 , 4 ) ( 7, 2 ) ( 5 , 2 ) ( 5 , 4 ) ( 7 , 4 )$
I $( 7 , 4 ) ( 4, 4 ) ( 4 , 7 ) ( 7 , 7 ) ( 7 , 4 )$
J $( 7 , 4 ) ( 7, 1 ) ( 4 , 1 ) ( 4 , 4 ) ( 7 , 4 )$
K $( 7 , 4 ) ( 3, 4 ) ( 3 , 8 ) ( 7 , 8 ) ( 7 , 4 )$
L $( 7 , 4 ) ( 7, 0 ) ( 3 , 0 ) ( 3 , 4 ) ( 7 , 4 )$
M $( 7 , 4 ) ( 2, 4 ) ( 2 , 9 ) ( 7 , 9 ) ( 7 , 4 )$
But this isn't all of the squares. Mrs Simmons class also found these:

And here are the coordinates:
A $( 7 , 4 ) ( 6, 5 ) ( 7 , 6 ) ( 8 , 5 ) ( 7 , 4 )$B $( 7 , 4 ) ( 8, 5 ) ( 9 , 4 ) ( 8 , 3 ) ( 7 , 4 )$
C $( 7 , 4 ) ( 8 , 3 ) ( 7 , 2 ) ( 6 , 3 ) ( 7 , 4 )$
D $( 7 , 4 ) ( 6, 3 ) ( 5 , 4 ) ( 6 , 5 ) ( 7 , 4 )$
E $( 7 , 4 ) ( 5, 6 ) ( 7 , 8 ) ( 9 , 6 ) ( 7 , 4 )$
F $( 7 , 4 ) ( 5, 2 ) ( 3 , 4 ) ( 5 , 6 ) ( 7 , 4 )$
G $( 7 , 4 ) ( 9, 2 ) ( 7 , 0 ) ( 5 , 2 ) ( 7 , 4 )$
H $( 7 , 4 ) ( 4, 1 ) ( 1 , 4 ) ( 4 , 7 ) ( 7 , 4 )$
Well done! You have obviously gone about this in a very logical way.
