Nonagon angle
Weekly Problem 53 - 2012
ABCDEFGHI is a regular nine-sided polygon (called a 'nonagon' or 'enneagon'). What is the size of the angle FAE ?
ABCDEFGHI is a regular nine-sided polygon (called a 'nonagon' or 'enneagon'). What is the size of the angle FAE ?
Age
11 to 14
Challenge level
Problem
Image
$ABCDEFGHI$ is a regular nine-sided polygon (called a 'nonagon' or 'enneagon').
What is the size of the angle $FAE$?
If you liked this problem, here is an NRICH task which challenges you to use similar mathematical ideas.
Student Solutions
$\angle FAE = 20^{\circ}$
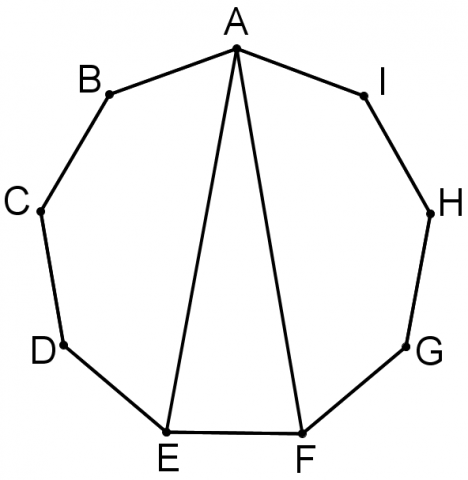
The interior angle of a regular nine-sided polygon = $180^{\circ} - (360^{\circ} \div 9) = 140^{\circ}$.
Consider the pentagon $ABCDE$: $$\angle EAB = {1\over2} (540^{\circ} - 3 \times 140^{\circ}) = 60^{\circ}$$ Similarly, $\angle FAI = 60^{\circ}$ and hence $\angle FAE = 140^{\circ} - (60^{\circ} + 60^{\circ}) = 20^{\circ}$.
Alternatively, the nonagon can be inscribed in a circle with center $O$. The angle $\angle EOF = \frac{360^{\circ}}{9} = 40^{\circ}$. By the circle theorems, $\angle EAF = \frac{40^{\circ}}{2} = 20^{\circ}$.
Image
The interior angle of a regular nine-sided polygon = $180^{\circ} - (360^{\circ} \div 9) = 140^{\circ}$.
Consider the pentagon $ABCDE$: $$\angle EAB = {1\over2} (540^{\circ} - 3 \times 140^{\circ}) = 60^{\circ}$$ Similarly, $\angle FAI = 60^{\circ}$ and hence $\angle FAE = 140^{\circ} - (60^{\circ} + 60^{\circ}) = 20^{\circ}$.
Alternatively, the nonagon can be inscribed in a circle with center $O$. The angle $\angle EOF = \frac{360^{\circ}}{9} = 40^{\circ}$. By the circle theorems, $\angle EAF = \frac{40^{\circ}}{2} = 20^{\circ}$.