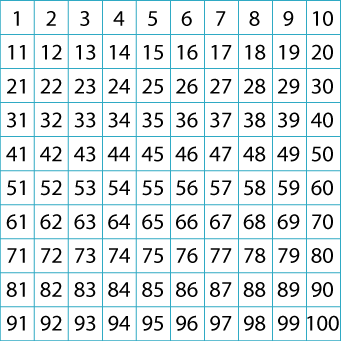
Hundred Square
A hundred square has been printed on both sides of a piece of paper. What is on the back of 100? 58? 23? 19?
Problem
A hundred square has been printed on both sides of a piece of paper. One square is directly behind the other.
What is on the back of $100$? $58$? $23$? $19$?
Can you see a pattern?
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Click here for a poster of this problem.
This problem is also available in French: Grille de 100
Getting Started
Can you imagine the square on the back? Where will its $1$ be? Where will its $10$ be?
So what will be on the back of the $20$ in the $100$ square in the picture? The $30$? Does this help with the $100$?
You could print off the $100$ square, or draw your own, and write just, for example, $1-10$ on the back of it to get you started. Can you see where $11-20$ would be? Perhaps this helps to predict the other numbers.
Student Solutions
We received many good solutions for this challenge.
Mikey from Archbishop of York CE Junior School wrote:
Having printed the page out I realised that if you turned it over you could see through the page. Looking where $100, 58, 23, 19$ would be meant you could read off the answers as $91, 53, 28, 12$. Or is this cheating?
I don't think this is cheating at all Mikey! Mikey then realised something else which was also spotted by "N" (he or she didn't give us a full Christian name):
If you draw a mirror line down the middle of the square you will be able to work out what number will be behind each number. You choose a number, then find its mirror on the other side of the line, this 'mirror' number will be the number on the reverse!
This is also a very handy method - well noticed. "N" sent an image with the "mirror line" drawn in:
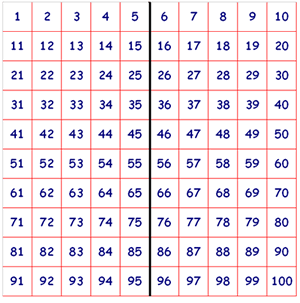
Devonshire Maths Club, Devonshire Primary School have found a pattern which they describe:
St Non's Class at St Mary's in Wales wrote:
We found this problem interesting and challenging.
Behind 100 would be 91. Behind 58 would be 52. Behind 23 is 28 and lastly behind 19 would be 12.
We counted how many space from the left it was, if it was 4 from the left it would also be 4 spaces in from the right.
We also knew that 5 was in middle and it would be matched with a 5 on the other side.
We tried adding the numbers on opposite sides together. We noticed that 1+10 = 11, 11+20 = 31, 21+30 = 51 and so on. These numbers went up in 20s.
We then tried the next line in 2+9 = 11, 12+19 = 31, 22+29 = 51.
These numbers also went up in 20s. We thought this was interesting.
We went to try the third row in 3+8 =11.... it was the same!!!
These are the patterns we noticed.
Thank you for information about the patterns that you found. I wonder whether you can explain why these patterns appear?
Teachers' Resources
Why do this problem?
This problem is an unusual way to explore number patterns in a well-known context. The activity will reinforce the construction of the hundred square, and increase children's familiarity with the sequences contained within it. Using a common resource, such as a hundred square, is a good way for children to begin to use visualisation, which they may find quite difficult at first. The act of visualising in this problem tests children's understanding of how the number square is created.
Possible approach
Key questions
What number is below $1$ on the hundred square?
Where will its $1$ be? Where will its $10$ be?
Possible extension
Learners could use a mirror on the hundred square and note all the patterns they can find. What happens if you add each number on the front to the number behind it? Using a different square such as a [$64$] $8$ by $8$ square will produce a different, if related, set of numbers.
Possible support
Many children will find this task more accessible if they have a real copy of a hundred square to use and annotate as they feel fit. [This sheet has two hundred squares on it.]