Far horizon
An observer is on top of a lighthouse. How far from the foot of the lighthouse is the horizon that the observer can see?
Problem

The radius of the Earth is 6367 kilometres.
An observer is on top of a lighthouse which is 25 metres high.
How far from the foot of the lighthouse, measured on the surface of the Earth, is the horizon that the observer can see?
It is 32 kilometres (21 miles) across the Channel between England and France and you can see France from the cliffs of Dover.
How high must the cliffs be for it to be possible to see that distance?
After finding the distance along the surface of the Earth from the foot of the lighthouse to the horizon, Clare used Pythagoras' Theorem to find the distance from the top of the lighthouse to the horizon.
What is this distance? Can you explain what you notice?
Getting Started
The observer's line of vision is along a tangent to the surface of the earth at the far point she can see on the horizon. Imagine a right angled triangle with the observer at one vertex, the far horizon point at another vertex and the centre of the earth at the third vertex.
You have enough information to find the angles in this triangle and hence the distance required.
Student Solutions
The solution below is based on the one sent in by Barinder of Langley Grammar School. We had quite a number of correct, well laid out solutions to this problem this month including those from Roy of Allerton High School, Dan (no address given) and Calum of Wayland High School.

Although definitely not in proportion, this makes the problem seem a lot easier. The question is asking for the length of the arc I have coloured red. To get this, I decided to find the angle $ \theta $ on the diagram, and use the equation
Arc Length $ = \frac {\theta}{360} \times 2 \pi r $ where $ \theta $ is measured in degrees and r is the radius.
$\angle OAB = 90^\circ$, since it is where a tangent and a radius of a circle meet - it is a circle theorem.
Thus, the triangle AOB can be drawn as follows:

We can now use trigonometry to find $ \theta $:
$$\begin{align*} \cos \theta &= \frac {6367000}{6367025} \\ \cos \theta &= 0.99999607 \\ \theta &= \cos^{-1} (0.99999607) = 0.1606^\circ \mbox{(4 d.p.)}\end{align*}$$
Substitute this into the equation for the arc length of a circle earlier to obtain the length required:
Arc Length $= \frac {0.1606}{360} \times 2\pi r. $
Arc Length $= 0.000446 \times 2 \times \pi \times 6367000 = 17,842.3m = 17.8 km $
The cliffs of Dover
For this next part, we are given the arc length, since this corresponds to the distance between England and France. The diagram is therefore:

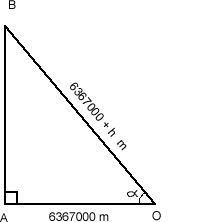
Thus, the cliffs of Dover are $80.4$ metres high.
Clare's distance
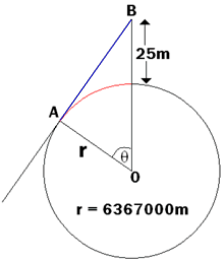
In this case, Clare has found the distance AB, shown in blue on this copy of the original diagram.
Using Pythagoras' Theorem,
$AB^2+6367000^2=6367025^2$
$\Rightarrow AB^2+40538689000000=40539007350625$
$\Rightarrow AB^2=318350625$
$\Rightarrow AB=17842.3828...\approx17842.4$ metres
This is very similar to the red distance, which we found to be $17842.3$ metres - they only differ by about $5$ cm!
To explain why these distances are so similar, a more representative diagram is helpful. Really, the lighthouse is very small compared to the Earth, and we found that $\theta=0.1606^\circ$, so the triangle should be very skinny!
In the diagram below, the lighthouse is still too big relative to the Earth as the angle is still several degrees (rather than $0.1606^\circ$), but you can see that the blue and red distances must be similar.
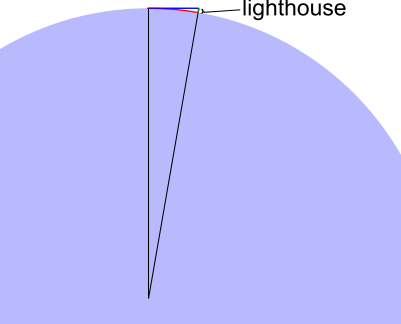
What happens as the lighthouse gets even smaller relative to the Earth? That is, as $\theta$ gets even closer to $0$?
Teachers' Resources
It is not envisaged that this problem would be used as a class problem. It is more appropriate for an enthusiastic student or small group of students looking for a challenge to work on independently.
