Proper Factors
Can you find the smallest integer which has exactly 426 proper factors?
Problem
A proper factor of an integer $N$ is a positive integer, not $1$ or $N$, that divides $N$.
- Show that $3^2\times 5^3$ has exactly $10$ proper factors. Determine how many other integers of the form $3^m\times5^n$ (where $m$ and $n$ are integers) have exactly $10$ proper factors. It might be easier to start by considering the total number of factors, rather than just the proper factors. You can also consider some simpler cases first to get a "feel" for the problem. How many factors are there of $3$, $3 \times 5$ and $3^2 \times 5$?
- Let $N$ be the smallest positive integer that has exactly $426$ proper factors. Determine $N$, giving your answer in terms of its prime factors. One way to get some insights into how to tackle this part is to consider a simpler case first. Can you find the smallest positive integer which has exactly $10$ proper factors? Note that we don't have to restrict ourselves to numbers of the form $3^m \times 5^n$, we could have powers of $2$, $7$ etc.
STEP Mathematics I, 2009, Q1. Question reproduced by kind permission of Cambridge Assessment Group Archives. The question remains Copyright University of Cambridge Local Examinations Syndicate ("UCLES"), All rights reserved.
Getting Started
It might be easier to start by thinking about the total number of factors (so include $1$ and $N$).
How many factors are there of:
- $3$
- $3 \times 5 = 15$
- $3^2 \times 5 = 45$?
Can you spot any patterns to help you find the total number of factors of $3^2 \times 5^3$?
What are the total number of factors of $3^m \times 5^n$?.
Student Solutions
Show that $3^2\times 5^3$ has exactly $10$ proper factors. Determine how many other integers of the form $3^m\times5^n$ (where $m$ and $n$ are integers) have exactly $10$ proper factors.
Dylan from Brooke Weston and Ishaan from Simon Balle All-Through School, both in the UK, used factorisations to count the number of proper factors of $3^2\times5^3.$ This is Dylan's work:

Prem from Cranford Community College in England used a table to count the proper factors, and to find a formula for the total number of proper factors:
To find the amount of "co-ordinates" on our graph we can simply do our length $\times$ width but we have to remember to subtract $2$ since a proper factor cannot be $1$ or $N.$

This makes the second part rather easier to visualise as we extend both axis of our graph to an arbitrary pair of values of $m, n.$ The total possible co-ordinates is still given by the same formula - our length would be $m + 1$ and our width would be $n + 1$ giving the total possible amount of pairs as $(m + 1)(n + 1)$ but as before, we have to subtract the top left and bottom right pairs as they would multiply to give us $1$ and $N$ which does not satisfy the conditions of a proper factor. $\Rightarrow$ the amount of proper factors $z = (m + 1)(n + 1) − 2.$
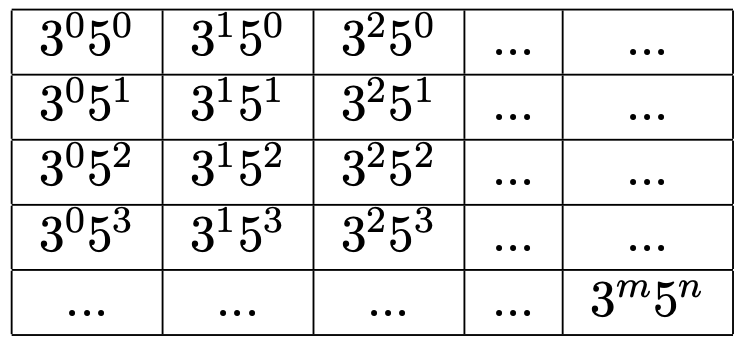
Nishad from Thomas Estley Community College in the England, Xuan Tung from HUS High School for Gifted Students in Vietnam, Natal from Canada, Dylan and Ishaan found the same formula without using a table. This is Xuan Tung's work:


Joshua from Bohunt Sixth Form in the UK, Ong from Kelvin Grove State College Brisbane in Australia, Nishad, Xuan Tung, Natal, Prem, Dylan and Ishaan used this formula - or these ideas - to count how many other numbers of the form $3^m\times5^n$ have $10$ proper factors. This is Ong's work:

There are two more possibilities that Ong missed but Nishad found:
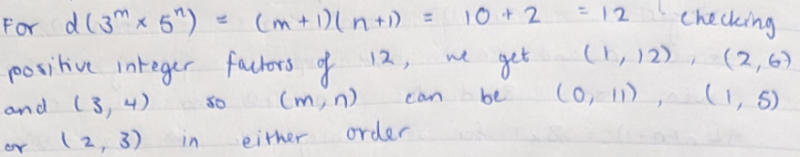
So $3^0\times5^{11}$ and $3^{11}\times5^0$ also have $10$ proper factors.
Ziwei (Gilbert) from Stowe School in the UK and Dibyadeep from Greenhill School in the USA counted up the factors in a different way. This is Ziwei (Gilbert)'s work (click on the images to open larger versions):
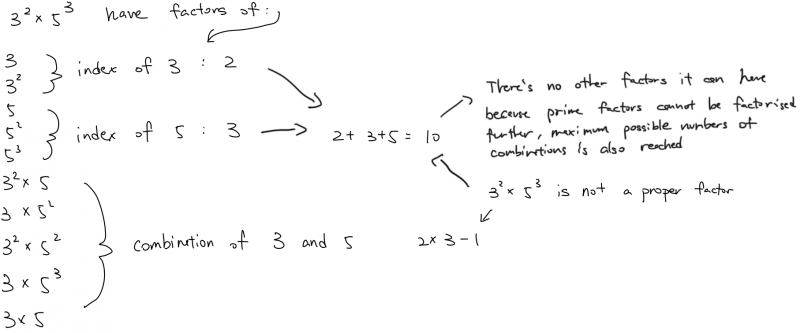

Let $N$ be the smallest positive integer that has exactly $426$ proper factors. Determine $N$, giving your answer in terms of its prime factors.
Joshua, Ishaan and Ong used the formula to find $N.$ They all assumed that $N$ would have three distinct prime factors. This is Ishaan's work:

Nishad, Dibyadeep, Xuan Tung, Dylan and Natal used a similar method, but they did not assume anything about the number of distinct prime factors of $N.$ This is Dibyadeep's work:


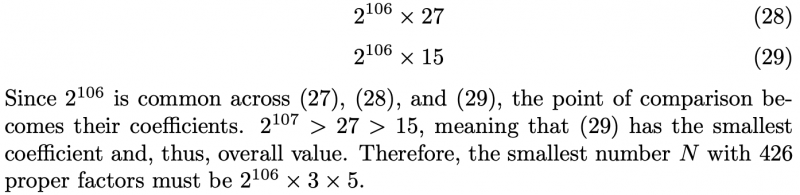
Dylan's method was shorter:

Natal explained why $N$ should have three distinct prime factors. This is Natal's work (click on the images to open larger versions):


Teachers' Resources
Why do this problem?
This problem requires pupils to think about prime number factorisation in different ways. There is no A-level content required to answer this question, but it does require careful and logical thought.
Pupils may find it easier to consider the total number of factors first, before moving onto proper factors.
Possible approach
Start with the first part of part 1, i.e. ask students the question "Show that $3^2\times 5^3$ has exactly $10$ proper factors". Ask students how they might approach this. Some ideas might be:
- Calculate the factors of $1125$ (having first worked out that $3^2\times 5^3=1125$)
- Work on some easier cases first, such as $3$, $3 \times 5$, $3^2 \times 5$, and see if this provides some insights into the problem
- Can the form $3^2\times 5^3$ be used to help answer the question? Can we use this form to work out what the prime factors are?
After considering this question, pupils can then find other numbers of the form $3^m\times 5^n$ which also have $10$ proper factors.
Before asking students to think about the question in part 2, they might like to try and find the smallest number which has exactly 10 proper factors.
Possible extension
Here is a list of number theory problems.
