Domino Square
Use the 'double-3 down' dominoes to make a square so that each side has eight dots.
Problem
These are the 'double-3 down' dominoes.

Use these dominoes to make this square so that each side has eight dots.

This task is designed to test your thinking! Do you have the resilience and the strategies to solve it?
Getting Started
Which dominoes could go on the same side as the double-3 domino?
It would be very useful to have some dominoes to move around, or you could print off and cut out them out from this sheet.
Student Solutions
Ethan, Texas, Andrew from Bandung Independent School in Indonesia wrote:
First, we tried to make 8 on one side of the square, but that didn't work out because the other sides couldn't be 8. We tried swapping dominoes around a few times, but still one side wouldn't add up to 8.
Then, we realized we could flip the dominoes around. The side that was 8 could stay 8, and that helped us to build the other sides.
Working as a group, we solved it quickly! Each one of us could solve one part, and we helped each other put the square together. We were faster than the teacher was!
Jack from St Gregory's school wrote:
I put the higher value dominoes in the middle of each arm then fitted the others around, adjusting using the pieces in the corners.
Cordelia, Esha and Mya from North London Collegiate School sent in their solution:
Here is our submission for dominoes that we did in our maths club:

Rihanna and Areebah from Gallions Mount School in Greenwich wrote:
First we got rid of the dominoes with the bigger numbers. Double-3 was the biggest one we put it in a row with dominoes with small numbers.
The dominoes with the blanks or ones were in the corners.
We checked that we hadn't used doubles [I think this means more than one of the same domino] by cutting out the dominoes to make sure we had used all the dominoes.
Andrew and Michael from Old Earth Primary, and Sam, Harry, Molly and Callum from St Nicolas C of E Junior School, Newbury started this challenge in the same way. Here is what Sam and Harry said:
Sam and I, Harry, counted all the dots on the double-3 down dominoes, so we got 30. But we needed 8 dots on each row and 8 x 4 = 32.
So we knew we had to put 2 dots in the corners because the dots in the corners count double because they are in two rows.
Andy and Michael expanded a bit on this:
All the corners must add up to 2, which is either 0, 0; 0, 2 or 0, 0; 1, 1.
In other words, the dots in the four corners must make a total of 2 dots. The only ways to have a total of 2 dots is by having one corner with 2 dots and the others all blank, or two corners blank and two with one dot.
Sam and Harry found this solution which had 2 dots in one corner and the other corners blank:
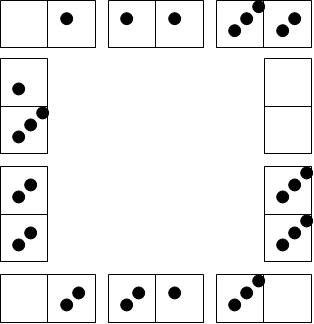
Thank you for all your contributions. I hope you'll send some again in the future.
Teachers' Resources
Why do this problem?
Dominoes are a great resource and this problem uses them in an intriguing and curious way. Not only does this activity require logical thinking but it is also an interesting way of practising addition and subtraction, and it provides an opportunity to talk about different ways of recording.
Possible approach
If you have an interactive whiteboard, you may find our Dominoes Environment useful for this problem.
You could introduce the challenge by laying out ten large dominoes in a square on the floor (it does not matter which dominoes go where). Ask the class to gather round and ask a few questions about the sum of dots on each side so that learners understand how the corner spots are counted in both the horizontal side and the vertical side.
Introduce the problem itself and ask pairs of children to talk for a minute or two about how they might tackle the problem. Share some of their suggestions among the whole group before giving them time to work in their pairs with dominoes. Using real dominoes whenever possible would be advantageous, but if that isn't possible then you could cut out some dominoes from our printable resources page. Squared paper would also be useful for jottings and recording.
As well as talking about the solutions in the plenary, you could focus on how children recorded their solutions. Some may well have just used the dominoes and moved them around as they went but how did they keep track of what they had tried? Some may have jotted down pictures of different arrangements. It would be useful to have a conversation about what ways of recording are most useful in this context.
Key questions
Possible extension
Use the 'double 4 down' dominoes to make a rectangle with equal numbers of dots on each side. Repeat with 'double 5 down' etc.
What numbers of dominoes can be made into a true square? Explore the numbers that emerge and explain why certain numbers of dominoes cannot be made into a square.
Possible support
Use real dominoes and sort out the '3 spot down' ones and use them to make a square. Then count the dots on the sides and work on the problem on a 'trial and improvement' basis.
You could start with the 'double 2 down' dominoes making each side add to 16 and using a square like this:

