Resilience and perseverance: the journey from novice to expert
This article reports findings from part of a wider NRICH project addressing ways to nurture and develop resilience and perseverance in the classroom. We would like to thank the schools who trialled our resources and shared their feedback.
Resilience and perseverance: The journey from novice to expert
Nurturing resilience and perseverance
Schools are often challenged to develop more resilient learners yet problem-solving requires much more than a willingness to 'try, try and try again.' Indeed, adopting such an approach can lead to learners feeling frustrated when their efforts appear unrewarded; no matter how hard our learners might try to solve a problem, they also need to recognise when their initial strategy might not be
working and develop a willingness to adopt a different approach. In other words, problem-solving often demands both resilience and perseverance. What might we expect from a novice compared to an expert? How might we support our learners' progress towards the expert level? At NRICH we've been working with teachers to develop and refine a collection of resources for supporting
learners to become more resilient. Let's begin by exploring our resilience and perseverance scale.
Progression in resilience and perseverance
Each of the four steps in our scale describes some of the behaviours that we might expect to see from learners working at that level. We recognise that it is unlikely that they will progress smoothly from one step to the next, they might fluctuate between them; schools tell us that this scale is most effective when it is based on a number of classroom observations. Here are the four steps:
- Step One: Getting started: these learners can state the key facts in a given problem, they understand what they need to find out and they can explain the task to another person.
- Step Two: Having a go: these learners are willing to make an initial attempt at the problem, perhaps using one of their known strategies such as working systematically, using trial and improvement, working backwards, making the problem simpler or simply having a guess.
- Step Three: Being resilient: these resilient learners do not give up easily with their chosen approach, they understand that making mistakes can help them to learn and make further progress. If they get stuck, or need to keep working for longer than usual on more challenging problems, their resilient attitude helps them to keep going.
- Step Four: Looking back: these resilient learners also realise that they might need to try more than one approach to solve a problem and they are willing to work flexibly. When they reach an answer, they check that their working out is correct and that their answer makes sense.
In this article we'll explore what these four steps might look like using solutions to a selection of NRICH activities. Let's begin with Twenty Divided Into Six (you might like to try this problem yourself before continuing to read the remainder of this article):

She arranged the cards into six piles.
The numbers on the cards in each pile added to the same total.
What was the total and how could this be done? Are you curious enough to find out?
Working with schools who trialled our resilience and perseverance resources, we have written commentaries illustrating how some their learners tackled this problem. Here's Mo's approach (please note, we have changed the names of the learners):
Where should we place Mo on our scale? His teacher tells us that Mo often rushes through mathematical tasks, aiming to finish as quickly as possible without wondering whether his answers make sense. For this problem, he knows that he needs to make six piles of cards but his have different totals. Mo does not appear to have taken the time to understand the challenge before he got
started. Without understanding a problem, he might struggle to become a more resilient learner even if he begins to accept that he should 'try, try, try again.' We suggest that Mo might benefit from being encouraged to focus on increasing his understanding of tasks by expecting him to state the key facts, putting the challenge into his own words or explain the challenge to another
learner before he tries to solve future problems.
Let's compare Mo's approach with Sarah's:
Sarah reads through the question. She highlights the key facts. She puts the challenge into her own words and explains it to her partner. Then, she stops working and asks for adult support.
Unlike Mo, Sarah appears to understand the task. We would suggest that Sarah's approach towards understanding a problem appears to place her on the first step of our progression. To become a more resilient learner, she needs to develop her confidence to 'Have a go' without initially relying on adult support. Working with teachers, we have found several ways to support learners like Sarah to
improve their resilience. For example, it can be effective to keep a list of known problem-solving strategies in their workbooks, or displayed on a classroom wall, which can help them to identify a possible way forward without adult support. For Twenty Divided into Six, both Mo and Sarah might explore using the trial and improvement strategy. Other possible
strategies they might consider in their future problem-solving lessons include:
- Working systematically (there will be more than one way of doing this)
- Pattern spotting
- Working backwards
- Reasoning logically
- Visualising
- Conjecturing
Not every problem has an obvious approach, though. Sometimes learners need a little more support. Working with focus groups of learners, we have found that they appreciate being able to access 'helpful hints.' These hints need to offer sufficient information to help to keep the learners on task without acting as 'spoilers.' Our NRICH activities often offer short hints for learners to
help them to build their problem-solving resilience.
Let's continue our discussion by exploring Sammy's approach to Twenty Divided into Six:
Sammy totals all of the numbers on her digit cards and divides the total by six. She decides that each pile must total 35. Sammy tries to organise her digit cards into six piles. Unlike some of the other members of her class, Sammy is not discouraged by realising she needs to place different numbers of digit cards in the various piles. She does not reach an
answer straight away, trying several different combinations before she finds a solution.
What does the commentary tell us about Sammy's resilience and perseverance? She appears to understand the problem and she is willing to 'Have a go' using the trial and improvement approach. She also appears willing to accept that making mistakes is part of her learning since we're told she makes making multiple attempts at organising her cards into piles totalling 35 without giving up. It
appears that she works with a minimum of adult support. We would suggest that the evidence places Sammy towards the higher end of the scale for this task. However, it is also important to remember that we are only looking at the evidence from a single activity; reflecting on a learner's resilience and perseverance over a range of activities, and different mathematical topics, might give a much
greater insight into their overall position along the scale and how best to support them.
Teachers tell us that some of their learners display different levels of resilience and perseverance for different strands of the mathematics curriculum; sometimes their learners are more likely to be resilient working with problems addressing geometry, measures or statistics than number and algebra. Investigating this further, it seems that some learners hold negative attitudes towards number
and algebra which possibly hinder their willingness to engage with problem-solving activities. Nevertheless, we believe that well designed resources can begin to overcome such hurdles. More specifically, we find that offering learners problems which have more than one possible approach towards their solution, as well as activities involving manipulatives or those that offer learners hints and
prompts, all support the development of more resilient learners with a willingness to persevere when facing an unfamiliar challenge. Let's explore each of these approaches in more depth, beginning with multiple approaches towards a problem.
The benefits of choosing problems with multiple approaches for nurturing perseverance
Although being resilient implies that an individual learner is willing to keep trying, we must remember that they might still get stuck or make a mistake. Also, they might need to be willing to change their overall approach to make further progress. This means that we need to choose classroom activities which have multiple approaches towards their solution to enable our learners to build both their resilience and perseverance. By sharing and discussing alternative approaches, learners will begin to develop a 'toolkit' of methods so they can make more informed decisions about which approach to take on future occasions. We have collected together some of our favourite activities with multiple approaches for primary and secondary learners. Let's explore how the following NRICH activity Different Deductions (primary version) and What's it Worth? (secondary version) uses multiple approaches to support both resilience and perseverance in the classroom:
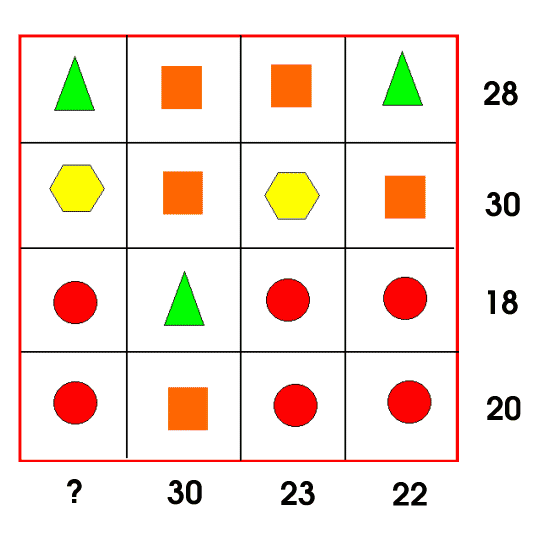
Each symbol has a numerical value. The total for the symbols is written at the end of each row and column.
Can you find the missing total that should go where the question mark has been put?
"I found out that a square is two more than a triangle. Then I worked it out from there that a square must be 8 and a triangle must be 6. I then worked out a circle was 4 because there was a gap of 8, and there were two circles in the line. Finally, I looked at the value of a hexagon. I worked out that I needed 14 more to make the line with 2 hexagons and 2 squares. I knew that the 2 squares made 16 so that left 14 for the 2 hexagons. I split 14 and it made 7. The final line was 7+6+4+4= 21."
Freya's solution highlights the benefits of offering learners a hint so that they can engage with a problem and develop the resilience to reach an answer. Freya adopts a 'What's the same, what's different?' approach towards her solution. However, not everyone who reaches a solution using the above hint takes the same approach as Freya. Here's a solution by Fred who attends Harris Academy Shortlands:
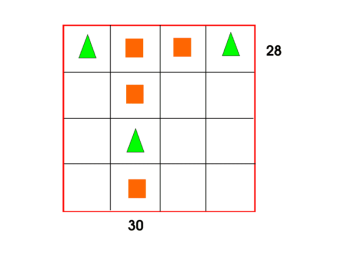
"I started with the "30" column. This column has the same shape three times and one different shape. It adds up to 30. I thought "what number goes into 30 three times with a bit left over?" First I tried 9 for the orange square and 3 for the green triangle: 9+9+9 = 27, 27 + 3 = 30. Then I filled in the numbers that occurred there everywhere else. I tested it with the top row which adds up to 28. 3 + 9 + 9 + 3 = 24. So that can't be right! Then I went back to my original column and tried some different numbers. 8+8+8 = 24, 24 + 6 = 30. So 8 and 6 would also work. I tried 8 and 6 in the top row and it worked: 6+8+8+6 = 28! Once I had done this I could work out the bottom two rows with the red circles. The circle is worth the same in both rows, the only difference is that one row has a green triangle and one has an orange square. For the bottom row, I took away the number I already knew from the total: 20-8 = 12. I knew that 3 circles = 12 so 12 divided by 3 gives you one circle be 4. Once you have three of the shapes you can work out the last one by adding down in the 23 column and working out what's left. To get the answer I added all the answers to the shapes together. 6 + 7 + 4 + 4 = 21. So the answer is 21."
Fred's use of trial and improvement is also an effective strategy for resilient learners, "First I tried 9 for the orange square...that can't be right!" He works carefully, displaying a willingness to check his answers and the resilience to go back and correct his mistakes.
Another way to support learners to 'Have a go' at a problem, once they have understood it, draws on the power of using the solutions on NRICH. Teachers tell us that sharing the first few lines of an NRICH solution with their learners can help them to recognise a familiar strategy and remind themselves how to get started. Later on, once they've reached a solution themselves, they could be encouraged to compare their efforts with the full solution on NRICH. To widen their range of strategies, learners could also be encouraged to look at other solutions to the same problem and see if they could follow them too.
As mentioned earlier, schools tell us that designing activities with on-screen hints is also an effective approach. Let's explore the activity Number Lines in Disguise which we believe maximises the potential of on-screen hints and tips:
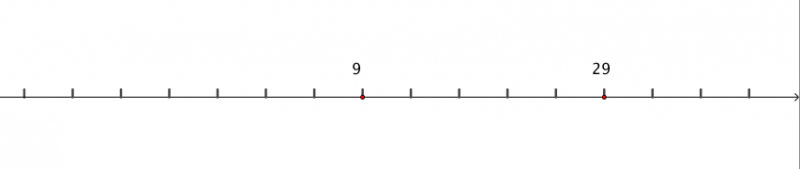
Number Lines in Disguise is designed to intrigue learners, it invites them to share what they notice. Teachers tell us that the interactive nature of challenge, coupled with the option of suggested questions or strategies to support further progress without necessarily requiring adult support, enables most of their learners to work independently on this problem. The interactive nature of the activity is very engaging, and learners can increase the level of challenge as their ability to label the number line becomes more accurate. This activity allows learners to access hints if needed, but otherwise they remain unseen behind a button. First, the learners are prompted by the hint "Where would 0 be on the line?" This is followed by a hint which acknowledges that it's OK to get stuck, even if you're a mathematician, and suggests a way forward too: "Often if a mathematician is stuck they might try an example with smaller numbers. Click below to reveal another example." The activity continues in a similar vein, offering short prompts to build resilience for problem-solving.
Oliver, from the Priory Academy LLST, shares his approach towards reaching a solution:
1) Count how many intervals there are between the two given values.
2) Find the difference between the two values and divide that by the number of intervals.
3) Keep adding the result from the first value, until you reach the required missing value.
Eg:
_ _ _ _ _ 12 _ ? _ 60 _ _ _ _ _
In this example, there are 4 intervals between the 12 and 60. The difference between 12 and 60 is 48, so we divide 48 by 4. This gives us 12. The missing value is two intervals ahead of 12, so we must add 12 two times. The answer, therefore, would be 36!
We mentioned earlier the power of using solutions on NRICH. In this case, the first part of Oliver's solution could be shared with other learners struggling to 'Have a go,' it offers an approach without giving away an answer.
So far we have focused our attention on examples of activities drawing on the number and algebra aspects of the curriculum. Let's consider a different curriculum topic by exploring a geometry activity.
Estimating Angles offers a similar approach to Number Lines in Disguise by encouraging learners to work in a resilient manner:
You can either play on your own or challenge a friend.
The closer you get to the target angle the more points you will score.
There are four levels:
Level 1: 0-90 degrees
Level 2: 0-180 degrees
Level 3: 0-270 degrees
Level 4: 0-360 degrees
There's also an additional opportunity with this resource, and for many other NRICH resources, for learners to pit their skills against an opponent (which could be a peer or the computer). Teachers tell us that the competitive aspect of this activity supports the development of their learners' perseverance when an individual's initial choice of approach is less successful than their opponent's, forcing them to reconsider their approach if they wish to be more successful in the next game.
Encouraging individual responsibility towards becoming more resilient learners with the perseverance to succeed
During this project, we found that another effective strategy for developing resilience and perseverance involves encouraging every learner to take more individual responsibility for their own learning. More specifically, one of the teachers placed a copy of the resilience and perseverance scale in the front of each workbook in the class. The learners were encouraged to reflect on their resilience and perseverance after each activity and suggest their own position on the progression, making sure that they could justify their reasoning. To help the learners make future progress, their teacher also asked them to consider an action which would help them work at the next level. The class had frequent opportunities to develop their resilience and perseverance over the term. During a feedback session, the learners were very positive about using the scale themselves and working their way along it. A number of learners who were initially working towards the lower end of the scale explained that they were keen to use prompts such as 'find the key facts' and explain 'What's the same, what's different' to help them progress. Several learners initially working at the third step proudly shared how they had tried using multiple approaches (rather than a single approach) and did not give up when they got stuck or made a mistake, realising that they were working towards the fourth step. In each case, the learners understood that they needed to become more resilient and to develop a willingness to work more flexibly to become better problem-solvers.
Our own actions can be incredibly effective agents for change. Research indicates that teacher modelling can be a very powerful strategy for encouraging learners to adopt new ways of solving problems. Some schools set aside staff meetings or PD sessions to explore problem-solving activities as a staff and reflect on their own problem-solving approaches, perhaps noting preferred strategies and comparing different approaches. Back in the classroom, those teachers shared with their learners how they needed to draw on their own resilience and perseverance to solve problems. You can access a huge range of suitable activities for professional development sessions, and accompanying articles which offer further background notes and teaching suggestions, by exploring our primary and secondary features.
Working with a number of schools during this project has highlighted the importance of ensuring regular classroom opportunities for developing resilience and perseverance. However, there are a number of other avenues to explore beyond the classroom such as lunchtime or after-school maths clubs and masterclasses. Many of our NRICH Roadshow activities are ideal for those events; each of these activities comes complete with accompanying teacher notes and an equipment list is provided for helping colleagues to organise the necessary resources.
Conclusion
This article has highlighted a selection of classroom tried-and-tested approaches for nurturing more resilient learners who are willing to persevere when faced with a non-routine problem. Choosing resources with multiple approaches, offering hints and encouraging learners to reflect on their existing skills as well as setting their own targets are all useful approaches towards building more resilient learners. If you would like to explore more activities designed to build resilience and perseverance in the mathematics classroom, our primary and secondary 'Being Resilient' collections are organised by curriculum strand. You might also enjoy this article about resilience and a growth mindset by Sue Johnston-Wilder and Clare Lee which was written especially for NRICH.
