Being Resilient - Primary is part of our Developing Mathematical Habits of Mind Primary collection.
In Developing Students' Resilience, we offer you support and advice on how to encourage your learners to become resilient mathematicians.
We know that good thinkers are resilient, they don't give up easily, and are motivated to work hard and keep going when faced with challenges. Here are some problems that may require similar determination from your learners. You could warn your learners that the solutions may not be immediately obvious, and they may need to persevere. We hope that they will have the opportunity to appreciate that
success can be sweeter after a struggle.
Additionally you may find that these tasks support the development of other problem-solving skills and mathematical habits of mind, which you could choose to highlight as and when they arise.
You can browse through the Number, Measures, Geometry or Statistics collections, or scroll down to see the full set of problems below.
Being resilient - Primary statistics
Being resilient - Primary geometry
Being resilient - Primary measures
Inside triangles
How many different triangles can you draw which each have one dot in the middle?
Rolling that cube

Four triangles puzzle
Cut four triangles from a square as shown in the picture. How many different shapes can you make by fitting the four triangles back together?
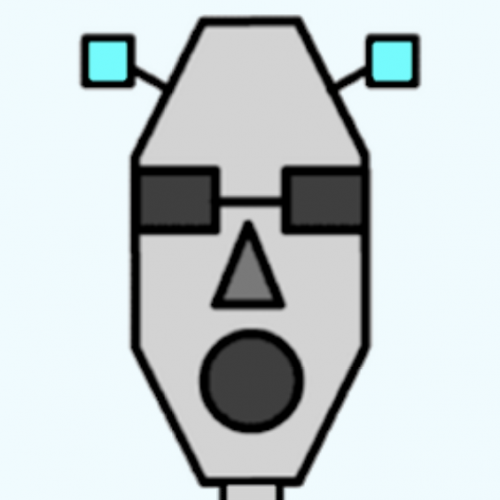
Robot monsters
Use these head, body and leg pieces to make Robot Monsters which are different heights.
Find the difference
Mixed-up socks
Start with three pairs of socks. Now mix them up so that no mismatched pair is the same as another mismatched pair. Is there more than one way to do it?
Make 37
Four bags contain a large number of 1s, 3s, 5s and 7s. Can you pick any ten numbers from the bags so that their total is 37?
Factors and multiples game
A game in which players take it in turns to choose a number. Can you block your opponent?
Dicey perimeter, dicey area
Which scripts?

How many times?
On a digital 24 hour clock, at certain times, all the digits are consecutive. How many times like this are there between midnight and 7 a.m.?
Nine-pin triangles
How many different triangles can you make on a circular pegboard that has nine pegs?
Number lines in disguise
Reach 100
Choose four different digits from 1-9 and put one in each box so that the resulting four two-digit numbers add to a total of 100.
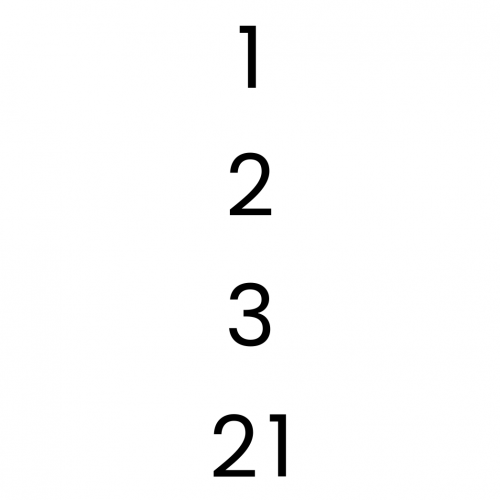
Factor lines
Arrange the four number cards on the grid, according to the rules, to make a diagonal, vertical or horizontal line.
Got it
A game for two people, or play online. Given a target number, say 23, and a range of numbers to choose from, say 1-4, players take it in turns to add to the running total to hit their target.
Two and two
How many solutions can you find to this sum? Each of the different letters stands for a different number.
