Triangle in a Square
Problem
This task is best done with at least one other person so you can talk through your ideas with someone else.
In the interactivity below, you can click through a series of mathematical statements made by Badger.
When each statement is revealed, your challenge is to decide whether or not it is true and why.
Talk to someone else about your thinking. Mathematicians don't like to take your word for it, they like to see a watertight chain of reasoning that covers all possibilities. Has Badger provided that?
If you are happy with a statement, you can click on 'OK' and the next statement is shown.
If you click on 'Pause' you have an opportunity to see some other children's thinking, which might help you form your own mathematical argument. Clicking on any of the examples of children's thinking will reveal Badger's response.
We would love to hear about your reasoning at each step. Can you use what you know about number and calculations to put together a watertight chain of reasoning that would convince a mathematician?
And perhaps you could create your own series of statements like this which includes some reasoning which isn't quite right? If you send us your statements, you may see them appear as an interactive task on NRICH!
Getting Started
If you click on 'Pause' in the interactivity, you can see some examples of other children's thinking, which might help you form your mathematical arguments.
You may wish to use some hands-on resources and/or sketch some pictures to help you.
Student Solutions
Thank you to everybody who sent in their ideas about this activity. Lots of children gave examples of triangles and squares which disprove Badger's last statement, and some children found ways of explaining why Badger is wrong.
Anna and Taylor from Westridge School in the USA sent us these pictures of triangles and squares:
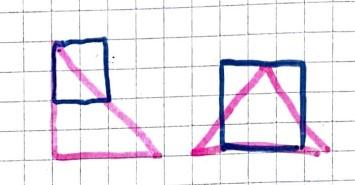
They said:
The step is wrong because a square can be smaller than a triangle but the triangle can't fit in the square.
These pictures clearly disprove Badger's fourth statement - well done.
Safina from Halstead Preparatory School in England used a real-life analogy to explain why Badger's reasoning is wrong:
It all depends on the size of both the square and triangle.
In 3 dimensions I cannot fit the Pyramids of Giza into my dice.
That's a good point! Even though a pyramid has fewer faces than a cube, I agree that the Pyramids of Giza are definitely bigger than your dice (unless you have a very big dice).
Lots of children agreed that the sizes of the triangle and the square matter. Some children thought that the type of triangle would make a difference as well. Charlotte, Sophie and Al from Westridge School said:
Not all triangles can fit in a square because size matters. Just because the amount of sides on a triangle are smaller then a square does not mean it always fits. There are different types of triangles, such as equilateral, isosceles, and scalene, which don't all fit in squares because of the length of the sides.
Have a look at Charlotte, Sophie and Al's full solution to see if you agree.
Haleema from Pierrepont Gamston Primary School in England also thought the type of triangle would matter. She said:
Badger's statements were all true until he got to the fourth one. This is because not all triangles are equilateral (meaning equal sides and angles when it comes to geometry). For example, a scalene triangle, in which no sides or angles are the same as another, wouldn't fit because in a square, all sides and angles are the same. For the scalene triangle to fit in any shape, that shape can not be a square.
Well done to all of you for using your knowledge of triangles to come up with hypotheses about whether or not they will fit inside squares. I agree that some triangles are awkward shapes and they seem like they would stick out of the sides of a square. This would make an interesting investigation - if you draw a triangle of each different type, can you also draw a big square around it? Or are there some triangles that will never fit inside any square?
We had lots of solutions which pointed out that a very big triangle could not fit inside a very small square. Where the sizes of the triangle and square are more similar, I wonder what it is that tells us that the triangle won't fit inside the square?
Ci Hui Minh Ngoc from Kong Hwa School in Singapore thought that it would be the area of the triangle and the square that made a difference. They said:
I can put some triangles in some squares but this is not because a triangle has fewer sides than a square. It is because of area!
This is a really good idea, Ci Hui Minh Ngoc. Is there any way of drawing a triangle inside a square where the area of the triangle is bigger? And is it possible to draw a triangle that doesn't fit inside a square even though the triangle has a smaller area than the square?
Amelie from Halstead Preparatory School thought that it would be the side length of the shapes that made a difference:
It doesn't matter about the amount of sides, only the side length of a shape. If a square has a smaller side length than a triangle, the triangle will not fit inside.
When I first read your solution I agreed with you, Amelie, but I've actually just managed to draw a triangle inside a square where one side of the triangle is longer than each side of the square. I wonder if anybody can find an example of this? Is it possible to draw a triangle inside a square where two sides of the triangle are longer than each side of the square? What about all three sides?
We also received excellent solutions from: Prayaan from King's College Junior School in the UK; Charlotte, Alyse, Charley, Kaitlyn, Xann and Stella from Westridge School; Dhruv from St. Anne's RC Primary School in the UK; Arya from Cubberley; Sion from Twyford School in the UK; Ryan from Kong Hwa School; and Teija and Fern from Pierrepont Gamston Primary School. Well done to all of you for investigating Badger's statements.
Teachers' Resources
Why do this problem?
The idea of this task is to give children the opportunity to critique a chain of reasoning. Having this experience will help learners to appreciate what constitutes watertight mathematical reasoning, so they can create their own proofs using words (and images, where appropriate).
This particular example of flawed reasoning also gives learners the chance to deepen their understanding of properties of 2D shapes.
The task An Easy Way to Multiply by 10? offers an identical structure but in the context of place value and calculation.
Possible approach
You may like to begin with a non-mathematical example of flawed reasoning:
Penguins are black and white.
Some old TV shows are black and white.
Therefore some penguins are old TV shows.
Give the class chance to talk in pairs about what is wrong with this, and use it as a springboard to introduce the task. Explain that being able to reason logically is a key skill for a mathematician, and the interactivity is going to give them the chance to 'unpick' someone else's reasoning.
Show the interactivity on the screen or whiteboard, with the Badger's first statement 'A triangle has 3 sides' showing. Invite learners to talk in pairs about whether they think that is true, and crucially, how they would use their mathematical knowledge to convince a mathematician that it was true, or not. Make sure everyone has access to a range of resources but try not to steer them in their choice.
Draw the whole class together to share ideas. If they are struggling to offer suggestions that convince you, click on the 'Pause' button and then reveal some other children's thinking. Do any of these examples give them a starting point? Which examples are not so helpful and why? Clicking on a particular example of children's thinking reveals Badger's response.
Continue in this way, giving everyone chance to consider each statement in turn. Only move on to the next statement when the class has a watertight mathematical argument to support or refute the previous one. In some cases, learners will come up with different chains of reasoning, not necessarily those in the examples, and that is fantastic. The key point is that the logic must be interrogated so that the class is satisfied it is correct.
Key questions
How do we know that statement is true (or not true)?
How could we check whether that statement is true (or not true)?
Are you sure that [this] follows on from [that]?
Possible support
Having a range of resources available, including access to pencils/paper/whiteboards/pens, will support all learners to access this task. Sharing the children's thinking built into the interactivity will help those who are struggling.
Possible extension
Diagonally Square offers learners the chance to create their own proof, but also includes a proof sorter, which will scaffold their thinking and help them appreciate the key features of a proof.
