Complex electricity

Producing electricity securely, safely, reliably and cheaply, has many challenges. Electricity is difficult to store in large quantities, so it usually has to be used as soon as it is generated. We also have a very low tolerance to any interruption in the electricity supply. Other challenges arise from the extreme interconnectedness of the electricity network, which means that a problem in part of the network quickly becomes a problem for the whole network.

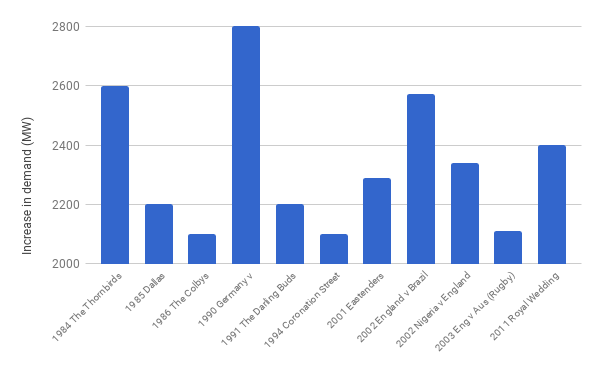
Most of the time the process of transmitting electricity proceeds smoothly. However, there have been times of such great demand that the UK electricity network has nearly been shut down, such as everyone boiling their kettles at half time during the 1990 World Cup semi final when England played Germany.

 

Image

Peak demands on the UK supply. (Data source National Grid)

The modern electricity supply network relies on the invention of alternating current (AC) by Nikolas Tesla. In AC the current and the voltage vary like a wave over time as seen below. Mathematically, these waves can be described by sine and cosine functions.

The AC voltage $V_{AC}(t)$ and current $I_{AC}(t)$ have the form $$V_{AC}(t)=|V|\cos (\omega t+{\varphi }_1),$$ and $$I_{AC}(t)=|I|\cos (\omega t+{\varphi }_2)$$ where $t$ is time, $\omega$ is the frequency of 50 Hz and $\phi_1$ and $\phi_2$ are the phases of the respective waves (the phase describes how far the wave is shifted along the horizontal axis), and $|V|$ and $|I|$ are the amplitudes of the respective waves (their heights).

Electricity is complex

To represent an AC voltage, electrical engineers make extensive use of complex numbers (you can explore complex numbers in Vanishing Roots). The imaginary number $i$ satisfies the equation $$i^2=-1$$

The reason for this is Euler's famous identity $$e^{i\theta }=\cos (\theta )+i\sin (\theta ).$$ which allows us an easy way of describing alternating current, along with its frequency and phase. (You can read more about Euler's identity here.)

Going back to our expression of the alternating $V_{AC}(t)$ above, we see that an alternating voltage is the real part of the function

$$V(t)=|V|\cos (\omega t+{\varphi }_1)+i|V|\sin (\omega t+{\varphi }_1)=|V|(\cos (\omega t+{\varphi }_1)+i\sin (\omega t+{\varphi }_1)).$$

This, according to Euler's identity, is equal to $$V(t)=|V|e^{i(\omega t+{\varphi }_1)}.$$ A convenient way to express this is as $$V(t)=|V|e^{i{\varphi }_1}{e}^{i\omega t}$$ and we call the expression $V=|V| e^{i\phi_1}$ the complex voltage. This single complex number contains two pieces of information, namely the amplitude, and the phase, of the voltage. There is a similar expression for the complex current. Expressing voltage and current as complex numbers makes the mathematics of power networks a whole lot easier, and is an important part of making sure that the lights always stay on.