Strolling along
What happens when we multiply a complex number by a real or an imaginary number?
Problem
This resource is part of our Adventures with Complex Numbers collection
This activity follows on from Opening the Door.
We can multiply a complex number by a real number or an imaginary number.
We just need to remember that $i^2=-1$. So, for example, $3i \times 4i=12i^2=-12$.
We have created the GeoGebra applet below for you to explore the questions that follow. You can move the complex number $z_1$, and $z_2$, which can either be real or imaginary, and the applet will show you their product, $z_3$.
Pick a complex number $z_1$, eg $4 + 2i$, and a positive real number $z_2$, eg 3.
What is $z_1 z_2$?
What happens as you change $z_1$ and $z_2$?
Can you describe geometrically the effect of multiplying by a positive real number?
What if $z_2$ is negative?
Now explore the effect of multiplying a variety of complex numbers by $i$ (set $z_2 = i$ in the Geogebra tool). Can you describe the effect geometrically?
Now try this for multiplication by $-i$.
What about multiplication by $2i$, $3i$, $-2i$, $-4i$, $\frac{1}{2}i$...?
Can you describe geometrically the effect of multiplying by any multiple of $i$?
Now that you've started to explore multiplication of complex numbers, you might like to step Into the Wilderness.
Student Solutions
Thank you very much to Pablo and Sergio from King's College Alicante in Spain, Z. Hakim from Annie Gale Jr High in Canada and Michele from Hockerill Anglo-European College in Italy, who all sent in good work on this problem. The solution below draws on their observations and explanations.
Multiplying by a real number
Here are some examples of multiplying a complex number by a positive real number:

$(3+2i)\times(3+0i)=9+6i$

$(3+2i)\times(0.5+0i)=1.5+i$
Multiplying $z_1$ by a real number $z_2$ enlarges $z_1$ by a scale factor of $z_2$, centred at $0+0i$.
The same happens if $z_2$ is negative, but this time the scale factor is negative, so $z_3$ is on the other side of $0+0i$:

$(3+2i)\times(-2+0i)=-6-4i$
Multiplying by $i$
Some examples are shown below. To help see the effect, the line segments joining $z_1$ and $z_3$ to $0+0i$ are also shown, and the right-angled triangles that these make with the axes are shaded.

$(0.9+5.8i) i=-5.8+0.9i$

$(-4.7+1.8i) i=-1.8-4.7i$

$(1.3-3.3i) i=3.3+1.3i$
Since in each case, the vertical side of one green triangle is equal to the horizontal side of the other and vice versa, the triangles must be congruent. So the distance from $0+0i$ to $z_3$ is the same as the distance from $0+0i$ to $z_1$. Also, the angle at $0+0i$ is the same in each pair of triangles, so the angles between their hypotensues must be $90^\circ$, the same as the angle between the real and imaginary axes.
So in each case, multiplication by $i$ represents a rotation of $90^\text o$ anticlockwise about $0+0i$.
We can use Pythagoras' Theorem to prove that the distance from $0+0i$ does not change.
e.g. For the first pair:
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{0.9^2+5.8^2}$.
We can use the gradients of the lines joining $z_1$ and $z_3$ to $0+0i$ to prove that they are perpendicular.
e.g. For the first pair:
The lines have gradients $\frac{5.8}{0.9}$ and $\frac{0.9}{-5.8}$
$\frac{5.8}{0.9}\times\frac{0.9}{-5.8}=-1$ so the lines are perpendicular.
We can also do this for a general complex number $z_1 = a+bi$:
$$z_3 = (a+bi)\times i=ai+bi^2=-b+ai$$
The distance of both $z_1$ and $z_3$ from $0+0i$ is $\sqrt{a^2+b^2}$
The gradients of the line segments joining $z_1$ and $z_3$ to $0+0i$ are $\frac ba$ and $\frac{a}{-b}$
$\frac ba\times\frac a{-b}=-1$, so they are perpendicular.
Multiplying by a multiple of $i$
Some examples are shown below.

$(-4-3i)\times(0+2i)=6-8i$
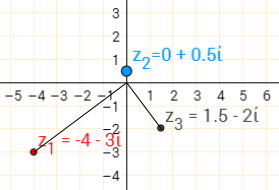
$(-4-3i)\times(0+0.5i)=1.5-2i$

$(-4-3i)\times(-3i)=12+9i$
The angle between the lines joining $z_1$ and $z_3$ to $0+0i$ are still perpendicular, so there is still a rotation of $90^\text o$ about $0+0i$. Notice that this rotation appears to be anticlockwise when $z_2$ is $2i$ or $0.5i$, but clockwise when $z_2=-3i$. So if $b$ is negative, then the direction of the rotation is reversed.
Also notice that $z_3$ is either closer to, or further from, $0+0i$ than $z_1$ is. So as well as a rotation, there is an enlargement centred at the origin. The scale factor of the enlargement is the size of $b$ - so when $b=2$ the scale factor is $2$, and when $b=-3$, the scale factor is $3$.
For positive values of $b$, this agrees with what we had seen so far, since multiplying by $bi$ is the same as multiplying by $i$ (rotation) and by $b$ (enlargement).
For negative values of $b$, we have said that the rotation is clockwise instead of anticlockise. We could explain this by saying that the enlargement has a negative scale factor, so everything is moved to the other side of the origin, which has the same effect as changing the direction of the rotation.
