Perimeter challenge

Lots of people submitted solutions to this problem - thank you everyone! There were too many good solutions to name everybody, but we've used a selection of them below: 

David from Sacred Heart Catholic College used algebra to solve part (a):

There are two values: $W$ (the width of the small rectangle) and $L$ (length of the small rectangle).

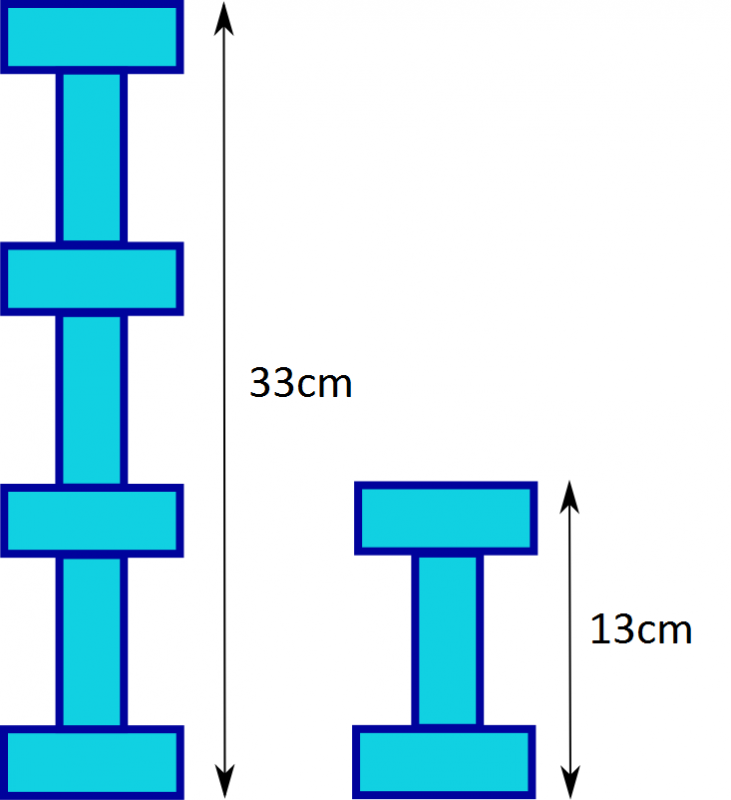
The height of the $1^{st}$ tower is made of $4W$ and $3L$, which equal $33$ ($4W + 3L = 33$)

The height of the $2^{nd}$ tower is made of $2W$ and only $1L$. They equal $13$ ($2W + L = 13$)

So If we double the second tower then we will have $4W$ but only $2L$. It will

equal $26$ ($4W + 2L = 26$).

Therefore if we take away double the second tower away from the first

tower, we will have one length and it will measure $7cm$. ($L =(4W + 3L) - (4W + 2L) = 33-26 =7$).

Now that we know what one length is, we can substitute $L=7$ into our equation for the height of tower $2$ ($2W + L = 13$).

If we take away the $7$ we will have $2W = 6$. Then you divide both sides of this equation by $2$ to find $W=3$.

To work out the perimeter, you will need to add $2W$ and $2L$.

This is $2\times 3 + 2\times 7$, equal to $\textbf{20cm}$.

Yueyang from CJS used a similar method to solve part (b):

You can see that there are five rectangles. Since their

combined area is $60cm^2$, this means that the area of one of the five

rectangles is $12cm^2$.

Then, we can see that the length of one rectangle

is the same as three widths. If $x$ is the length of the triangle and $y$ is the width, we can now form the equations:

$xy = 12$

$x = 3y$

Thus, we can substitute $x$ with $3y$, turning the first equation in to $3y^2 = 12$. Divide each side by $3$ to make $y^2=4$. The square root of $4$ is $2$, so the width of the rectangle is $2$. In that case, as $x$ is $3$ times $y$, the length of the rectangle is $6$. Therefore, the perimeter will be $2+6+2+6$ which is equal to $\textbf{16cm}$.

Here's how Care, Nika and Brian from British International School Phuket solved part (c):

If we call the length of the rectangle $b$ and the width $a$ then we can see $4a = b$.

Then the width of the big rectangle is $4a+2a=6a$ and the area is $6a \times 4a = 24a^2 = 600$.

Then $a^2 = 25$

So $a = 5mm$

$b = 4a= 20mm$

and perimeter of rectangle = $\textbf{50mm}$

Tyler, Katie, Jennifer, Peter and Zach from Lab School thought about factors to solve part (d):

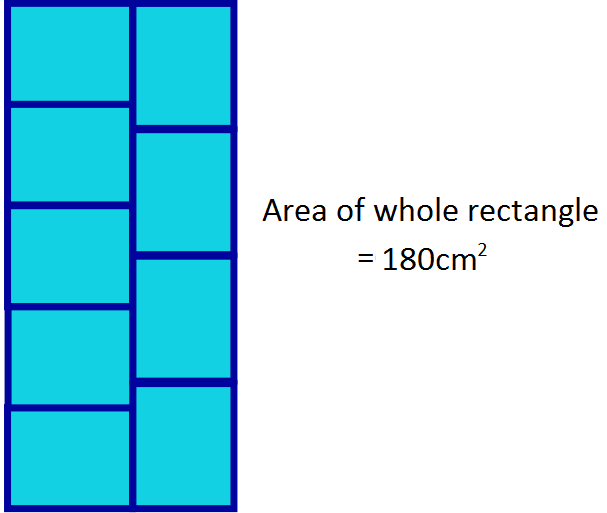
Step $1$: We read the area of shape (d), which was $180cm^2$.

Step $2$: We came up with the equation $x= \frac{4}{5}$ of $y$. In this equation $x$

represents the shorter side of the rectangle and $y$ represents the longer sides. This is

true because the height of the large rectangle equals either $5$ shorter sides or $4$ longer

sides.

Step $3$:  We found out that the area of each small rectangle is $20cm^2$,

because $9$ small rectangles equal $1$ large rectangle, and $180 \div 9=20$.     

Step $4$: We found all the factors of $20$ and paired them up: $1$ and $20$, $2$ and $10$, $4$ and $5$.

Step $5$: We found out that only one pair of the factors follows rule of one number being $\frac{4}{5}$ of the other. These factors are $5$ and $4$.

Step $6$: So the perimeter of the small rectangle is $4+5+4+5=18cm^2$.

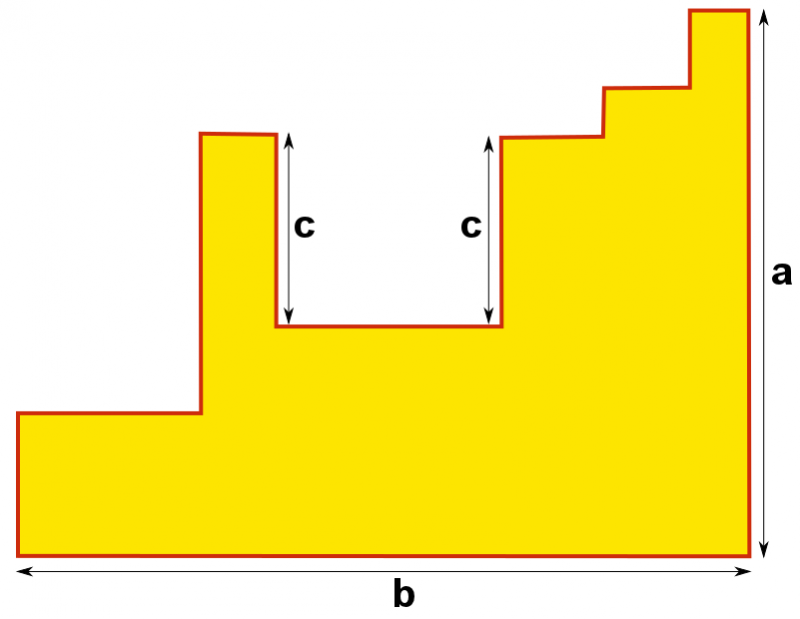
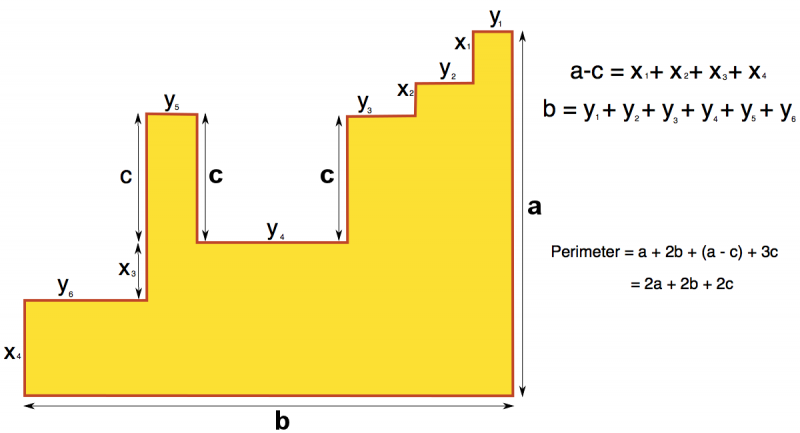
Paula and Kiera from Hinchley Wood drew a diagram to show how they found the perimeter of the final shape:

Image

Thank you again to everybody who submitted a solution!