Display boards
Problem

A Year 5 class wants to display the results of their problem solving in the school hall.
They need 32 display boards - one each - and they are wondering how to arrange them.
Rules for setting up the boards:
-
The boards can be joined in a straight line or at right angles.
-
The boards will fall if there are more than four in a straight line.
-
The final arrangement of the 32 display boards has to be a closed shape so that people can walk around the outside and view all the problem solving results displayed.
-
The hall floor has square tiles. Each board, which is as long as the square tiles, needs to be placed on the edge of one of these squares so that it stands up.
A. The kitchen staff would like to use the hall for school dinners. They would like the display to be as long and narrow as possible, and at one end of the hall.
B. Teachers would like to use the hall for PE. They would like the display to fit in a corner so that it leaves as much space as possible for PE.
Are the teachers right that the corner design takes up less space than the one at the end of the hall? Why or why not?
C. The Year 5 teacher thinks that the best viewing shape is the one that has as many long straight lines of four display boards in it as possible and they don't mind where it is in the room.
Further challenge
The headteacher would like the display to be very visible from whatever door people enter the hall. They would like the display to be as square as possible and in the middle of the hall.
A. Design a display for the headteacher that is as square as possible.
Explain how you have decided it is as square as possible.
B. Design a display for the headteacher that is as square as possible and has four lines of symmetry.
C. Design a display for the headteacher that is as square as possible, has four lines of symmetry and has an internal area of 40 square tiles.
How many arrangements can you find that fit these requirements?
This problem featured in a preliminary round of the Young Mathematicians' Award 2014.
Student Solutions
We haven't received many solutions to this task yet. The children below have tried to find the narrowest solution possible. If you think you've found a narrower one, please email us to let us know!
Some children at Beckwithshaw Primary School sent in their ideas. Ollie, Megan and Ryan said:
How we did it was we got 32 lolly sticks and placed them on 2 big sheets of A3 squared paper. After that, we looked for possible solutions keeping in mind the rules. We drew them in our books and came to the conclusion of 1 possibility. Our answer showed all the rules and was a closed space. It was hard to keep it as narrow as possible but with trial and error we eventually solved it.

Jack and David sent in this solution for the narrowest display board:
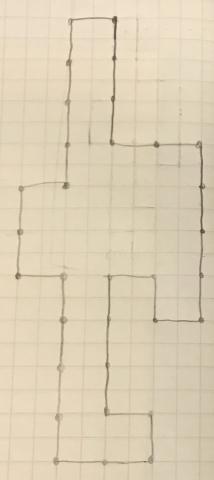
Thank you all for sharing your ideas with us. Interestingly, Ollie, Megan and Ryan's last shape has a smaller area than Jack and David's shape, but Jack and David's shape is 'narrower' in the sense that it is only four display boards wide at its widest point. I wonder which would be more helpful to have at the end of the hall?
Do you think it is possible to find an arrangement that is only three boards wide at its widest point? Or two?
Teachers' Resources
Why do this problem?
This problem puts the pupils in a spatial problem-solving situation. The amount of necessary knowledge is very little but perseverance in achieving the "best" arrangements will challenge many pupils.
Possible approach
Using 32 sticks/rods/matchsticks/straws have the children gathered around for a short discussion. It is good if you can use a squared background (flooring/large sheets of fairly big squared paper). If you are presenting this to a small group of pupils then 2cm squared paper can be used together with cut straws. It would be good to be able to represent a much larger space than the
arrangement can cover so as to represent the whole of a school hall. The arrangement can be used to discuss the rules that are to be applied, particularly the "closed shape" and the sticking to the sides of squares.
Following this start the pupils may be given access to many different pieces of equipment to help, particularly squared paper for recording.
Key questions
Tell me about what you're doing.
How did you decide that this is the best for ...?
Possible support
Some pupils may need help with moving the "display boards" around and keeping them in the position they've chosen. Some may need help with recording their ideas.
