Play to 37
In this game the winner is the first to make the total 37. Is this a fair game?
Problem
This is a game for two players.
Each bag above has unlimited 1s, 3s, 5s or 7s in it.
Watch the video to see how Charlie and Liz play the game and then adapt it to set themselves new challenges. Alternatively, you can scroll down to read the rules and get started.
Aim of the game:
To be the player to add the final number to the 'running' total to make 37.
How to play:
- Decide who is going first.
- Player 1 chooses one of the numbers from the bags above (1, 3, 5 or 7).
- Player 2 then chooses a number from one of the bags and adds this onto Player 1's number to make a running total.
- Player 1 then has another turn and again, chooses a number from one of the bags, and adds it to the running total.
- Play continues like this with each player choosing a number and adding it onto the running total, until one player reaches the target of 37.
Play the game a few times. What do you notice?
Is this a fair game? Do both players have an equal chance of winning? Why, or why not?
Here's a slightly different version of the game...

This time, each bag above has unlimited 2s, 4s, 6s or 8s in it.
The aim is to be the player who reaches 30.
Play the game a few times. What do you notice?
Is this a fair game? Do both players have an equal chance of winning? Why, or why not?
Would having a target of 34 make any difference?
If you have bags of 2s, 4s, 6s and 8s, and you are given a target number, how will you decide whether it is better to go first or second?
Student Solutions
The children from Irvinestown Primary School in the UK thought hard about this problem. Emily, Lexie, Adele, Anna, Lily and Olivia said:
It isn't fair. The person who goes first always wins.
You're right, this does seem to happen. I wonder why?
Kaumudi and Siddharth from Ganit Kreeda in Vichar Vatika, India had some ideas about this. Kaumudi said:
When a person lands their opponent into number 36, 34, 32, 30, they will win. Why? If they land the opponent into 36, they will choose 1 and win. If they land the opponent into 34 they will choose 3 and win. Same goes for 32 and 30. For 32 they will choose the number 5 and for 30, 7.
Siddharth went back one step further:
After we played for some time, we noticed that 27 and 29 were the danger numbers in the game. What danger number means is that whoever has to play their turn on this number will lose, as whatever number they play will make them lose. If the person has to play a turn on the number 27, and they play 1, it will be 28. The opponent can then play the sudden loss number, 29. If they play 3, they will make 30, which the opponent will add 7 to win. If they add 5, it will be 32, which the opponent will play 5 to win. If the person plays 7, it will be 34, which the opponent will play three on to win. If you play any number on 29, you will lose instantly. So the person who plays first usually has the advantage.
Wren from Pierrepont Gamston Primary School in England looked at some possible ways of making 37, and used that to work out why the first player always wins:

Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia also noticed that the total at the end of Player 1's turn will always be odd, while the total on Player 2's turn will always be even. They sent in this explanation:
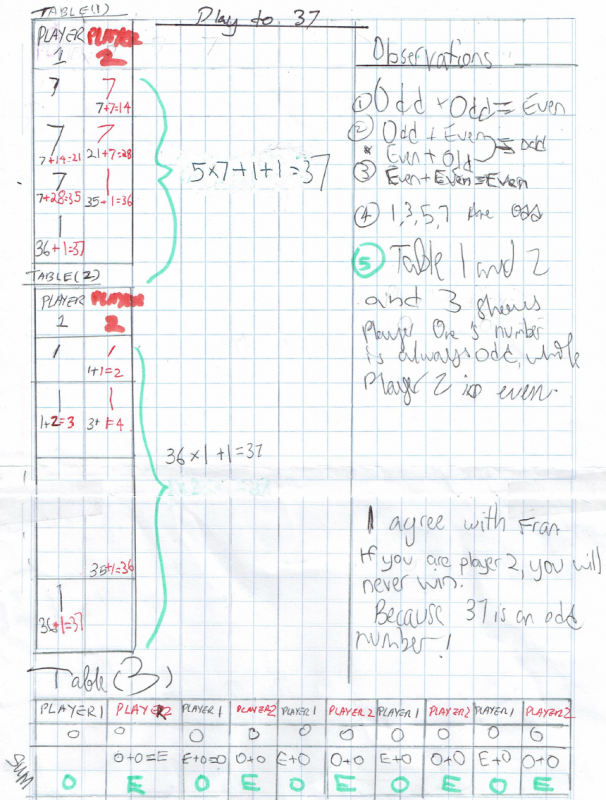
Well done for explaining that - I am now convinced that Player 1 will always win because Player 2 can't get to an odd number on any of their turns.
Siddharth also worked out why going second gives you the advantage for the version with the second set of bags, where the target number is 30:
If you play the version with 2, 4, 6, 8, and the target being 30, 20 and 10, it will be the danger zone, as the numbers pair up to be 10, so if you play eight on 20, your opponent will play two and vice versa and the same for 6 and 4. So the person who plays first will always win.
If the score target is 34 however, it is a game of chance.
Siddharth is right - because the numbers pair to 10, the second player can always make the total a multiple of 10! There is actually a way for the first player to use this information to their advantage in the version of the game where the target is 34 - can you see what it is?
Ci Hui Minh Ngoc also looked at the different possible numbers of moves in the first game. They found that the lowest number of moves is 7 and the largest is 37, and they also found ways of getting to 37 using 9, 13 and 19 moves. I wonder which other numbers of moves are possible between 7 and 37?
The children at Greenwich Public School in Australia thought hard about this. Their teacher said:
They hypothesised that every odd number between 7 (smallest number of numbers to 37) and 37 (largest number of numbers to 37) is able to be used to reach 37. This was after we had all pairs play the game and feedback how many numbers they used to get to 37. They noticed a pattern of all moves being odd. They systematically checked many of the answers (9, 11, 13, 15, 17, 19, 21, 25) before they reached the hypothesis that each odd number would work.
Well done for spotting a pattern and making a hypothesis! I wonder why the game can last any odd number of moves between 7 and 37?
Teachers' Resources
Why play this game?
At a basic level, this game provides an opportunity for children to become more fluent in addition. In order to try to win, learners will need to think ahead and this element of strategy demands higher-order thinking. Stepping back to analyse different versions of the game offers yet more challenge, and the chance to generalise when it is better to start the game and when it is better to go second.
Possible approach
In the video that accompanies the problem (and in the recording above), Liz and Charlie are trying to model how you might interact with students in your class. You could watch the video(s) and adapt what you do according to the age range you are working with.
Alternatively, you could show the problem video to your class, pausing when recommended to offer some thinking and playing time, and to facilitate discussion.
Key questions
Do both players have an equal chance of winning the game? Why or why not?
How do you decide whether you want to start, or go second?
Possible support
The game Nim-7 would make a good starting point.
Possible extension
The game Got It would make a good follow-up challenge.
