Identities
-

-
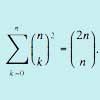 problemFavourite
problemFavouriteBinomial
By considering powers of (1+x), show that the sum of the squares of the binomial coefficients from 0 to n is 2nCn -
 problemFavourite
problemFavouriteCubes within cubes revisited
Imagine starting with one yellow cube and covering it all over with a single layer of red cubes, and then covering that cube with a layer of blue cubes. How many red and blue cubes would you need? -
 problemFavourite
problemFavouritePartitioning revisited
We can show that (x + 1)² = x² + 2x + 1 by considering the area of an (x + 1) by (x + 1) square. Show in a similar way that (x + 2)² = x² + 4x + 4
-
 problem
problemPowerful factors
Use the fact that: x²-y² = (x-y)(x+y) and x³+y³ = (x+y) (x²-xy+y²) to find the highest power of 2 and the highest power of 3 which divide 5^{36}-1. -
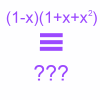 problem
problemParticularly general
By proving these particular identities, prove the existence of general cases.
