Cubes within Cubes revisited
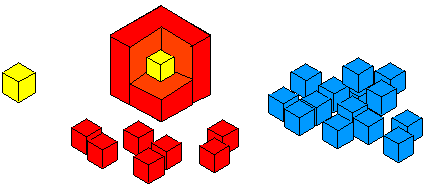
This is then covered with a layer of blue cubes.
How many red cubes have you used?
How many blue cubes have you used?
Find an easy way of working this out.
Now imagine adding a layer of green cubes.
How many green cubes are needed?
Have you a quick method for working out the amounts that you would need for each layer?
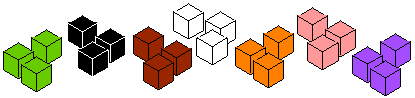
Martha thought about the third layer like this:
- The whole of the new cube is a $5$ by $5$ by $5$ cube.
- The inner layers made a $3$ by $3$ by $3$ cube.
- So the new layer is $5^3 - 3^3 = 125 - 27$ cubes.
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Emma made the third layer like this:
- First she added a $5$ by $5$ plinth to the bottom, and another to the top.
- Then she added a $3$ by $3$ block to each vertical face, and finally four columns of $3$ cubes to the corners.
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Charlie made the third layer like this:
- First he added a $3$ by $3$ block to the top and another to the bottom.
- Then he made lots of pillars of $5$ cubes, and wrapped $16$ of these round the sides
Can you see it like this?
Using this method, if you have an $x$ by $x$ by $x$ cube, can you explain how to find an expression for the number of cubes needed to make the next layer?
Can you show that all three expressions are equivalent?
Can you find another way to think about this problem?
Show how you form your expression, and show that it is equivalent to the examples above.
Yanqing from Devonport High School for Girls sent us a complete solution to this problem:
These are all equivalent.
Another way of thinking about the problem is:
First you put a square with side of $x$ on each face ($6x^2$ cubes), then a column of $x$ cubes on each edge ($12x$ cubes), and finally one cube on each corner ($8$ cubes).
This would give us our $6x^2 + 12x + 8$ expression, which is what you get when you simplify the other expressions.
Well done Yanqing.
This problem demonstrates how a formula can be derived from the context (rather than "pattern-spotting") in a variety of ways.
It also provides practice in the manipulation of algebraic symbols and generates generalities that can promote discussions on equivalent symbolic forms.
A teacher comments:
This was a good opportunity to practise simple and more difficult sequences and generation of formulae, ranging from linear to cubic. All pupils were able to access the problem up to (and beyond) their own "natural" ability (Year 9 set 2).