Window frames
Problem
The windows in my house have six panes of glass. They are three panes wide and two panes high.
Here is a simplified drawing of a window in my house. Can you see how many small pieces of edging it uses?
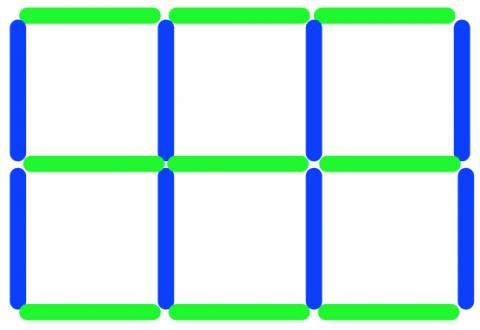
The pieces of frame go around the edge of the panes, so we call them 'edging pieces'. They are all the same length and there are 17 of them.
The picture above shows the edging pieces - there are 9 green pieces going across and 8 blue pieces going up.
Challenge 1
Explore other rectangular windows which are one window pane wider than they are high.
How many edging pieces do you need? (We need 17 in the example above.)
How many panes of glass are there altogether? (There are 6 in the example above.)
Explore the numbers you get as you make the windows bigger.
Challenge 2
In this picture, we can see the inside edging pieces coloured blue and the ones surrounding the shape coloured green:
This gives us 7 inside blue pieces and 10 surrounding green pieces, making 17 altogether.
Have another look at the rectangular windows from Challenge 1, which are one window pane wider than they are high.
What numbers can you get for the inside and surrounding pieces?
Using the numbers you've got from exploring rectangular windows (that are one wider than they are high), what things can you find out about those numbers? Below you can see how others started exploring.
This idea from Louis uses sloping lines:
Freya used her tables knowledge:
Petros used this idea for the areas of the windows:
Kia found a different way of looking at the little squares:
Student Solutions
Challenge 1:
31 edge pieces
12 glass panes
I got an odd number of edge pieces
Challenge 2:
There are 14 outside edge pieces and 17 inside edge pieces. Same number of edge pieces as above.
Challenge 3:
All the number of edge pieces are odd.
Formula to work out edge pieces without counting:
(Number of panes ×2) + (the height + the width)
Good ideas! I wonder how Dhruv has worked out that formula?
We also received lots of solutions from Ananya, Kanaa, Twisha, Niya, Valerie, Ved, Anika, Kimaya, Swara, Mrunmayee, Ayansh, Aarav and Shivashree from Ganit Kreeda, Vicharvatika. They used matchsticks to help them with this task.
Challenge 1:
All of the children worked out that the number of panes is equal to the product of the height and the width of the window.
Kanaa noticed that the total number of matchsticks goes up by 4 more each time the window size increases. She has used colours in the second picture to show why this happens. In the first picture, the column with the header 'number of frames' actually refers to the number of panes of glass. You can click on Kanaa's pictures to make them bigger.
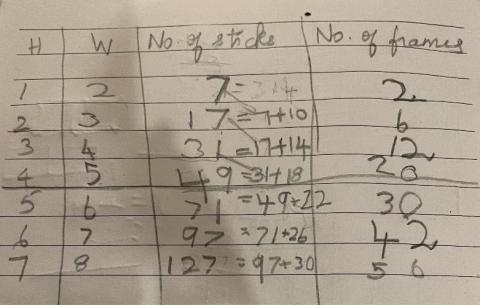
Mrunmayee used these calculations to work out the number of edging pieces in the 4 by 5 window:
4 × 5 = 20
20 + 20 = 40
40 + 4 + 5 = 49
Aarav, Niya and Ayansh generalised this method, using h and w to represent the height and width of the window:
Total number of vertical sticks = (h + 1) × w
Total number of horizontal sticks = (w + 1) × h
Total number of sticks = (h + 1) × w + (w + 1) × h
They also found out that the total number of vertical sticks is always bigger than the total number of horizontal sticks by 1. These are some good ideas - I wonder if we can use the fact that the width of the window is always 1 more than the height to help us write a simpler formula for the total number of sticks?
Ayansh came up with another formula for the total number of sticks, which is the same as Dhruv's from earlier:
Number of sticks = 2 × panes + height + width
Well done for working this out! I wonder if this always gives the same answer as (h + 1) × w + (w + 1) × h?
Challenge 2:
Kanaa found the number of outside edging pieces by adding double the width to double the height. You can click on this picture to make it bigger.
Aarav explained that this is because for every window boundary, there are 2 horizontal lines each made up of sticks equal to its width and 2 vertical lines each made up of sticks equal to its height.
To find the inside edging pieces for the 5 by 6 rectangle, Kanaa added the width 4 times and the height 5 times. I wonder if this method can be developed into a general formula to find the number of inside edging pieces for a rectangle of any size?
Thank you all for sending in your ideas. You've worked very hard on this task. To see some more of these children's ideas, take a look at Ganit Kreeda's full solutions.
If anybody would like to add to any of these solutions or send in any new suggestions, please email us.
Teachers' Resources
Window Frames
The windows in my house have six panes of glass. They are three panes wide and two panes high.
Here is a simplified drawing of a window in my house. Can you see how many small pieces of edging it uses?
The pieces of frame go around the edge of the panes, so we call them 'edging pieces'. They are all the same length and there are 17 of them.
The picture above shows the edging pieces - there are 9 green pieces going across and 8 blue pieces going up.
Challenge 1
Explore other rectangular windows which are one window pane wider than they are high.
How many edging pieces do you need? (We need 17 in the example above.)
How many panes of glass are there altogether? (There are 6 in the example above.)
Explore the numbers you get as you make the windows bigger.
Challenge 2
In this picture, we can see the inside edging pieces coloured blue and the ones surrounding the shape coloured green:
This gives us 7 inside blue pieces and 10 surrounding green pieces, making 17 altogether.
Have another look at the rectangular windows from Challenge 1, which are one window pane wider than they are high.
What numbers can you get for the inside and surrounding pieces?
Using the numbers you've got from exploring rectangular windows (that are one wider than they are high), what things can you find out about those numbers? Below you can see how others started exploring.
This idea from Louis uses sloping lines:
Freya used her tables knowledge:
Petros used this idea for the areas of the windows:
Kia found a different way of looking at the little squares:
Why do this problem?
This task provides an introduction to the ideas of area and perimeter, while allowing children to practise their counting skills and spot patterns in numbers. It encourages a systematic approach and provides an opportunity for pupils to explain how they know they have all the solutions. This task gives children the opportunity to pursue their curiosity, asking questions
like "I wonder what would happen if I...?"
If curiosity is something you're developing in your classroom then the videos mentioned at the bottom of this page may be useful.
Possible approach
Begin by showing pupils a model similar to the blue and green version in the second picture. Discuss what children notice. Can they talk about the 'panes' and the 'edges'? How many of each can they see? Explain how the blue and green lines are different, and make sure that all pupils understand what the words 'height' and 'width' mean.
When pupils have understood these ideas, give them time to make the window frames and count the 'edging pieces' and 'panes'.
After each challenge, bring the whole class back together to discuss what number patterns they can see. The pictures in Challenge 3 can be used as prompts to encourage children to think of different ways of exploring these patterns.
Key questions
Tell me about how you are doing this challenge.
Are you checking your answers? How?
Possible extension
Use other windows when the longer side may be more than 1 unit longer than the narrower side. Encourage children to explore patterns, keeping the length and width of the windows no bigger than 6.
Ask children to investigate the following challenge: If you have 90 edging pieces to use, what window sizes can you make if you are allowed to use the pieces to make more than one window? Can you make windows which are all different where the number of edging pieces adds up to exactly 90?
e.g.
1 by 3 = 10, 2 by 4 = 22, 4 by 6 = 58 makes 90 altogether
1 by 6 = 19, 2 by 4 = 22, 4 by 5 = 49 makes 90 altogether
Wire Cages is a 3D version of this task.
Possible support
Some pupils may need support with working out which edging pieces to count. Providing simple models for children to move around would be helpful for all pupils.
Teacher support for curiosity
This task was created to help younger pupils pursue their curiosity within maths lessons. If you'd like any support with sparking curiosity in your pupils, these videos might be helpful.
Firstly "The Rise & Fall of Curiosity", particularly the extract [23.50 - 37.15] on "adult encouragement answering and teacher behaviour."
Secondly, "The Hungry Mind: The Origins of Curiosity", particularly the extract [8.22 - 12.29] on "Children asking questions"

First can also be found at - https://www.youtube.com/watch?v=X-0NOrIU67w
Second can also be found at https://www.youtube.com/watch?v=Wh4WAdw-oq8