What Salt?
Problem
Have you ever wondered why common salt is NaCl rather than NaCl$_2$ or NaCl$_3$? Here's your chance to investigate this mystery!
In case you haven't seen a Born-Haber cycle before, one is illustrated below for LiF:
[http://en.wikipedia.org/wiki/File:BornHaberLiF.PNG]
Using the data below, construct a Born-Haber cycle for NaCl and NaCl$_2$ . Calculate the lattice enthalpy for NaCl, and the enthalpy of formation of NaCl$_2$
$\Delta H_f(NaCl)$ = -411 kJ mol$^{-1}$
$\Delta H_{latt}(NaCl_2)$ =-3360 kJ mol$^{-1}$
$IE_1(Na)$ = +496 kJ mol$^{-1}$
$IE_2(Na)$ = +4563 kJ mol$^{-1}$
$EA_1(Cl)$ = -349 kJ mol$^{-1}$
$\Delta H_{sub}(Na_{(s)})$ = +108 kJ mol$^{-1}$
$\Delta H_{at}(\frac{1}{2}Cl_{2\ (g)})$ = +121 kJ mol$^{-1}$
From looking at the signs and relative magnitudes of the two calculated enthalpies of formation, can you explain why NaCl$_2$ is not formed?
What are the major contributing factors in the mathematical expression for the enthalpies of formation which makes the formation of NaCl$_2$ so unfavourable? What does this tell you about the likely formation of NaCl$_n$, where n > 2 ?
As you may have guessed by now, the contsruction of Born-Haber cycles are quite laborious, and also rely solely upon experimentally determined enthalpy values. In many cases these enthalpy values may not be present, and so a reasonable prediction of a lattice enthalpy can be calculated by the Born-Lande expression (which is shown below). This equation assumes that ions are hard spheres held
together solely by electrostatic attractions.
$$E = -\frac{N_AMz^+z^-e^2}{4\pi \epsilon_0r_0}(1-\frac{1}{n})$$
where:
$E$ is the lattice enthalpy
$N_A$ is Avogadro's number ($6.023 \times 10^{23}$)
$z^+$ is the charge on the cation in electron units
$z^-$ is the charge on the anion in electron units
$e$ is the charge on an electron ($1.602 \times 10^{-19} C$)
$4\pi \epsilon_0 = 1.11 \times 10^{-10} C^2/(J m)$
$r_0$ is distance to closest ion
$n$ and $M$ are constants for a given lattice
Using the data below, use the Born-Lande equation to calculate the lattice enthalpies of AgCl, AgBr and AgI.
$M$ = -1.74756
$n_{AgCl}$ =10.5
$n_{AgBr}$ = 11
$n_{AgBr}$ = 12
$r_{Ag^+}$ =115 pm
$r_{Cl^-}$ = 181 pm
$r_{Br^-}$ = 196 pm
$r_{I^-}$ = 220 pm
$\Delta H_{latt}(AgCl)$ = -915 kJ mol$^{-1}$
$\Delta H_{latt} (AgBr)$ = -904 kJ mol$^{-1}$
$\Delta H_{latt} (AgI)$ = - 889 kJ mol$^{-1}$
Comparing these values of the lattice energies to those calculated using the Born-Haber cycle, for which of the lattices does the Born-Lande equation give a good approximation?
Why is there a degree of discrepancy between the two approaches for calculating the lattice enthalpy? Why does this discrepancy increase with larger halides?
Getting Started
Having constructed the Born-Haber cycles, and having worked out the relevant data, look at how the two cycles differ. There should be one key point that changed enormously, to make the formation of NaCl$_2$ so unfavourable. Think what the change would be for a NaCl$_3$, and whether this would be offset by the lattice enthalpy. Generally, we can draw a conclusion for NaCl$_n$...
Although the Born-Lande equation will be new to almost everyone, this question involves little more than plugging in given data to the equation. Note that the Born-Lande calculates lattice enthalpies based on a purely electrostatic model, and consequently always underestimates the true lattice enthalpy. What extra factor hasn't been taken into account? Why would this factor increase for larger halides?
Student Solutions
The Born-Haber cycle for NaCl is shown below:
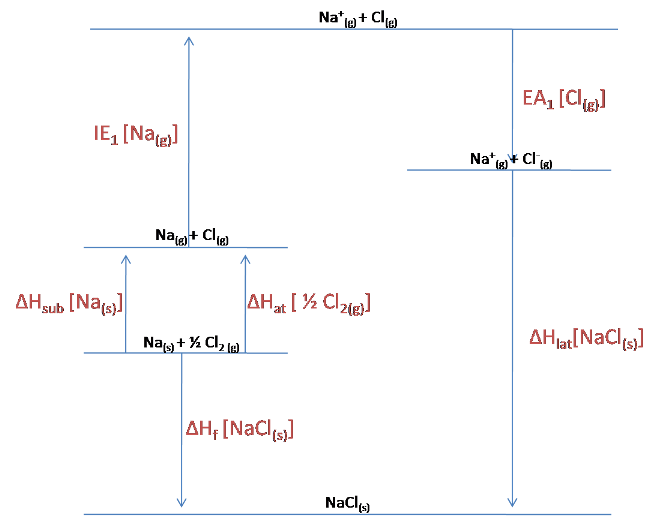
As can be seen from the diagram:
$$\Delta H_{lat}[NaCl_{(s)}] = -EA_1[Cl_{(g)}] - IE_1[NA_{(g)}] -\Delta H_{sub}[Na_{(s)}] -\Delta H_{at}[\frac{1}{2}Cl_{2\ (g)}] + \Delta H_f [NaCl_{(s)}]$$
$$= 349 -496 -108-121 -411$$
$$= -787\ kJ/mol$$
For NaCl$_2$, the following Born-Haber cycle can be constructed:
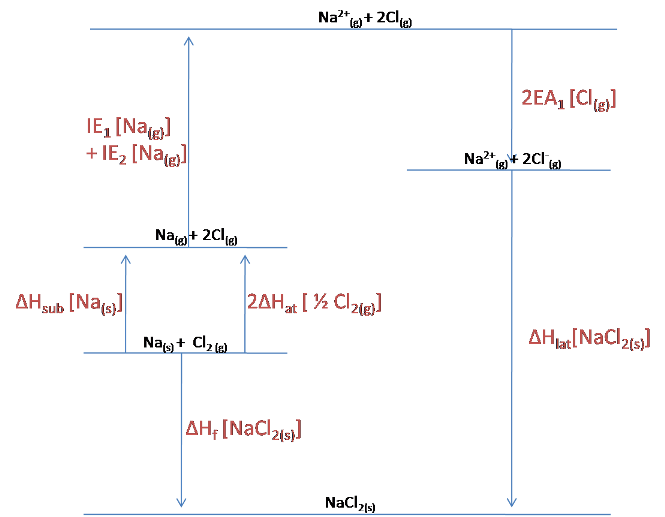
The lattice enthalpy is already given in the question, but we can still use the cycle to calculate the enthalpy of formation of NaCl$_2$.
$$\Delta H_f [NaCl_{2\ (s)}] = \Delta H_{sub}[Na_{(s)}] + 2\Delta H_{at}[\frac{1}{2}Cl_{2\ (s)}] + IE_1[Na_{(g)}] + IE_2[Na_{(g)}] + 2EA_1[Cl_{(g)}] + \Delta H_{lat}[NaCl_{2\ (s)}]$$
$$= 108 + 2(121) + 496 + 4563 +2(-349) +(-3360)$$
$$= +1351\ kJ/mol$$
As this calculation reveals, the enthalpy of formation of NaCl$_2$ is actually endothermic (positive) rather than endothermic (negative), and so the drawn Born-Haber cycle is actually incorrect. The cycle should reveal that the lattice is higher in energy than the elements that it is formed from.
It is clear to see that NaCl$_2$ actually requires energy to be formed from its constituent elements, whereas NaCl releases energy upon its formation. This is the main reason why NaCl is formed preferentially over NaCl$_2$, since it is lower in energy.
The main contribution that makes the formation of NaCl$_2$ so unfavourable is the large second ionisation energy of sodium. The excessive amount of energy that needs to be put in to remove an electron from an already positively-charged ion means that the overall formation of the lattice is not favourable. Because subsequent ionisation energies are even higher (which are not compensated for by the increased attraction in the lattice), it is likely that the formation of other NaCl$_n$ lattices are even more unlikely.
Simply by plugging the correct ionic radii and born exponents into the Born-Lande equation should yield the results shown below. Alongside are the lattice enthalpies calculated experimentally, for comparison:
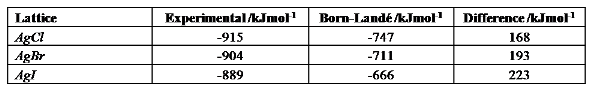
It can be seen that the Born-Lande equation gives a reasonable approximation for the smaller of the halides, but that as the halide size increases, the discrepancy between theoretical and experimental lattice enthalpies changes. It should be noted foremost that the theoretical value is always lower than the experimental, since it relies solely on electrostatic interactions: there are of course additional covalent forces which strengthen the lattice. The increasing discrepancy for increasing size of halide indicates that the larger halides have an increased amount of covalent bonding, which is not taken into account by the Born-Lande equation. Covalent bonding is the sharing of electrons, and it can be rationalised that increased covalent character is seen for the larger halides, since these halides are more diffuse and so have more polarisable electron densities.
