Two's company
Seven balls are shaken. You win if the two blue balls end up touching. What is the probability of winning?
Problem
Two's Company printable sheet - problem
Two's Company printable sheet - recording sheets
A container holds $4$ yellow marbles, $2$ blue marbles and $1$ red marble.
The marbles are identical in all ways except colour.
Run the interactivity below to simulate shaking the container.
You win if two blue marbles touch.
Did you win?
Complete several shakes and look at your results.
Approximately how often do you think you would win if you completed $100$ throws?
Make a prediction and then check it by doing the experiment.
Can you find a way of working out the theoretical probability of winning?
You may find these Recording Sheets useful.
Getting Started
In how many different positions can the two blue marbles settle?
How many of these positions contain the two marbles touching?
These
Recording Sheets might be useful for finding all
possible combinations.
Student Solutions
Ahan from Tanglin Trust School in Singapore used probability. There is a small mistake in Ahan's work, which is explained.
There is a $\frac17$ chance that the first ball goes in the middle and whenever this happens we win.
There is a further $\frac16$ chance that the second ball lands in the middle. This too guarantees a win. In fact, this probability is $\frac67\times\frac16$, because for the second ball to land in the middle, the first ball must not land in the middle, which happens with probability $\frac67$.
To calculate the chance that 2 balls are next to each other we first must calculate the chance of it happening if both balls land outside the center. No matter where the first ball lands (outside the center) there are 5 places the second ball can land. If it goes in two of these you win. This means that the chance of winning when it lands outside is $\frac25$.
But since only $\frac{29}{42}$ of the time you don't get a middle (this probability becomes $\frac57$) the chance you win by to outside balls is $\frac{58}{210}$ (this becomes $\frac25\times\frac57 = \frac57$)
Add that to the $\frac{65}{210}$ that comes from having one in the center (which is actually $\frac27$) the probability of winning is $\frac{123}{210}$ or $\frac{41}{70}$ (which becomes $\frac47$).
Dashiell from Sequoyah in the USA found the numbers of ways there are to win and lose.
I did that by drawing seven marbles in a circle (one in the middle six surrounding it)
and then I numbered the marbles. For example, the two marbles that have a 1 [in] them are a winning possibility, same with the marbles with 2 [in them] and so on.
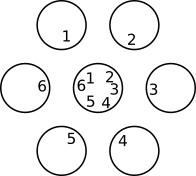


Then I did the same thing, but with losing possibilities.
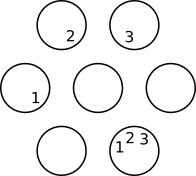
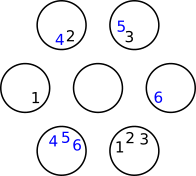
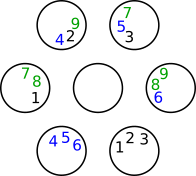
The winning possibilities was 12 and the losing possibilities was 9
12 + 9 = 21
$\frac{12}{21}$ = 0.571428
So 57.1428% is the probability of winning.
On the live problem I did the run 100 test. After that I added the mean for one hundred tries. Then two hundred, three hundred, and so on. The answer kept getting closer. The closest I got was 0.5714547933.
NS from TCS in the USA used factorials.
"Four factorial" is written $4!$ and means $4\times3\times2\times1$. There are $4!$ ways to arrange $4$ marbles in $4$ spaces because:
There are $4$ empty spaces in which to place the first marble
For each of these $4$ options for the first marble, there will be $3$ options left for the second marble
For each of these $4\times3$ arrangements for the first two marbles, there will be $2$ options left for the third marble, and only $1$ for the fourth.
This is NS' work:
Even though colors are interchangeable, lets work with numbering the balls $1$ to $7.$
There are $7!$ combinations.
Let's number the spots by row

Let's put Blue-$1$ Ball in spot $1$. There are $3$ adjacent spots where Blue-$2$ can be in order to be touching. Same for all the spots except spot $4$ which is center.
For each of the outer spots, total permutations possible are $1\times3\times5!$ ($1$ for the first blue ball, $3$ for the second, and $5!$ for the $5$ balls which are not blue)
Total for out spots = $6\times3\times5!$
For the center spot = $1\times6\times5!$
sum $=8\times3\times5!$
probability $=\dfrac{8\times3\times5! }{7!} = \dfrac{24}{42}$
We received one more solution which was not correct, but looks very convincing:
One of the blue balls will come at the edge of the container in order to be adjacent to another blue ball. Now, the other ball has three possible positions to fulfil the winning criteria:
• At the centre
• To the left side
• To the right side
The following rectangles represent the possible positions for the other blue ball.

After the first blue ball has arranged itself at one of the edge positions, there are 6 balls left which includes the other blue ball.
The probability that the other blue ball falls in the first box is $\frac16$
The probability that the other blue ball falls in the second box is $\frac16$
The probability that the other blue ball falls in the third box is $\frac16$
So the total probability will be the addition of the three probabilities
$\frac16+\frac16+\frac16 = \frac36 = \frac12 = 50\%$
The problem is that this only applies if the first blue ball lands in one of the edge positions. If, instead, the first blue ball lands in the middle, it doesn't matter where the second blue ball lands - you win regardless. The probability of this happening is $\frac17$.
The probability that the first blue ball lands in one of the edge positions is $\frac67$, so the probability that the first blue ball lands in an edge position and the second blue ball lands next to it is $\frac67\times\frac12 = \frac37$.
Total probability is still $\frac47$
Teachers' Resources
Why do this problem?
This problem offers an opportunity to explore and discuss two types of probability: experimental and theoretical. The simulation generates lots of experimental data quickly, freeing time to focus on predictions, analysis and justifications.
Possible approach
Demonstrate the interactivity by running it a few times, explaining that to win, the two blue balls need to touch.
Invite students to estimate the probability of winning. Allow students some thinking and discussion time in pairs before bringing them together to state their initial conjectures.
Students may find these Recording Sheets useful for exploring different possible outcomes.
Record their conjectures on the board and then run the interactivity a few hundred times.
Then revisit students' conjectures and discuss which ones matched the experimental data, before rounding the activity off by discussing which methods for recording the different combinations were both successful and efficient.
Key questions
Are there efficient systems for recording the different possible combinations?
What counts as a different outcome?
If the yellow and red marbles are in the same position but the blue marbles swap places, does that count as a different outcome?
Possible support
This problem could be tackled as a follow-up to Cosy Corner
Teachers may want to use this recording tool to gather the results of other similar experiments that their students are carrying out:
Possible extension
A follow-up problem could be The Better Choice
