Two circles

The required area is shown below in fig. $1$.

Image

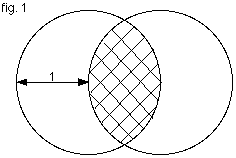
To find the area it may help to consider just one of the circles and the sector created.

The angle in the sector is $120$ degrees. (See fig. $2$.)

Image

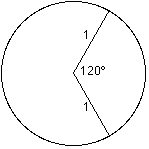
Hence the area of the sector is $\frac{120}{360} \times\pi \times1 \times1 = \frac{\pi}{3}$.

Now by considering the area of the triangle in fig. $3$, we can find the area of the shaded segment.

Image

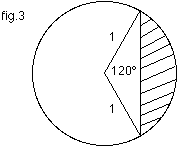
The area of the triangle $= 0.5 \times\sin 120^{\circ} = \frac{\sqrt{3}}{4}$ So the area of the shaded segment $= \left(\frac{\pi}{3} - \frac{\sqrt{3}}{4}\right)$ square units. The area of the overlap is twice this amount which is : $ 2\left(\frac{\pi}{3} - \frac{\sqrt{3}}{4}\right) = \frac{2\pi}{3} - \frac{\sqrt{3}}{2}$ square units.