Two and One
Problem
Two children are playing a game with three balls, two blue ones and one red one.
Terry is red and Ali is blue.
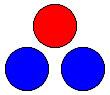
They toss up the balls, which run down a slope so that they land in a row of three, like this:
The colour in the middle wins that round. Is this a fair game?
Who do you think will win?
Why?
Try using the interactivity below to get a feel for the game. (The sum column tells you how many times Terry has won so far.)
Getting Started
Is it important that there is only red ball but two blue balls?
Student Solutions
We had some good solutions to this problem. Rukmini from Dowanhill Primary wrote:
You're right, Rukmini, well done. Nicholas who goes to Lochinver House School and Courtney from Holystone Primary expressed their solution in a slightly different, but equally as good, way. Courtney said:
It is not fair because Terry has a one in three chance but Ali has a $2$ in $3$ chance.
Teachers' Resources
Two and One
Two children are playing a game with three balls, two blue ones and one red one.
Terry is red and Ali is blue.
They toss up the balls, which run down a slope so that they land in a row of three, like this:
The colour in the middle wins that round. Is this a fair game?
Who do you think will win?
Why?
Try using the interactivity below to get a feel for the game. (The sum column tells you how many times Terry has won so far.)
Why do this problem?
This problem offers children the opportunity for children to get a feel for experimental probability and to work systematically to find all possible outcomes.
Possible approach
The interactivity will help children to get a feel for this problem. However they should be encouraged not only to identify a pattern in the data they collect, but also to explain why this pattern occurs.
The problem builds on the ideas of fairness introduced in Domino Pick and would benefit from discussion.
Of course this problem could also be tackled practically. Pupils themselves may throw the balls outside and collect data for the whole class.
Key questions
Why not find three balls so that you can try playing the game with a friend. What happens?
Is it important that there is only red ball but two blue balls?
How could you record what you have found out?
Would it be helpful to use some red and blue counters for working out the different possibilities?
Possible extension
Learners could try Tricky Track once they have had a go at this task.
Possible support
Suggest trying with real balls first. Some red and blue counters might be helpful for working out the different possibilities.